Ανισότητες από άλλες ανισότητες
Συντονιστής: chris_gatos
-
orestisgotsis
- Δημοσιεύσεις: 1753
- Εγγραφή: Σάβ Φεβ 25, 2012 10:19 pm
Ανισότητες από άλλες ανισότητες
ΠΕΡΙΤΤΑ
τελευταία επεξεργασία από orestisgotsis σε Παρ Φεβ 23, 2024 1:45 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Λέξεις Κλειδιά:
Re: Ανισότητες από άλλες ανισότητες
Η συνάρτησηorestisgotsis έγραψε: ↑Τρί Φεβ 20, 2024 1:40 pmΓια τους αριθμούςισχύει:
. Να αποδείξετε ότι:
α).
β).
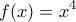 είναι κυρτή. Με τη βοήθεια του Θ.Μ.Τ. στα διαστήματα
είναι κυρτή. Με τη βοήθεια του Θ.Μ.Τ. στα διαστήματα ![\displaystyle{[a,b],[b,c], [c,d]} \displaystyle{[a,b],[b,c], [c,d]}](/forum/ext/geomar/texintegr/latexrender/pictures/020f30bf84fb3c69125474679558acad.png) έχουμε:
έχουμε: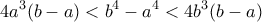 ,
, 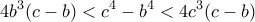 ,
, 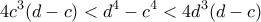
Προσθέτοντας κατά μέλη έχουμε τις ζητούμενες ανισότητες.


- matha
- Γενικός Συντονιστής
- Δημοσιεύσεις: 6423
- Εγγραφή: Παρ Μάιος 21, 2010 7:40 pm
- Τοποθεσία: Θεσσαλονίκη
Re: Ανισότητες από άλλες ανισότητες
Αποδεικνύονται αμέσως και με απλή χρήση της ανισότητας ΑΜ-ΓΜ.
Π.χ. για την πρώτη:
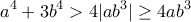
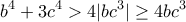
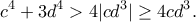
Με πρόσθεση λαμβάνουμε το ζητούμενο.
Από την απόδειξη αυτή φαίνεται ότι η διάταξη δεν παίζει κανέναν ρόλο, απλώς χρειάζεται να είναι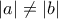 ή
ή 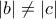 ή
ή 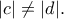
Με ανάλογο τρόπο αποδεικνύεται και η δεύτερη.
Π.χ. για την πρώτη:
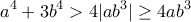
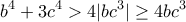
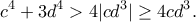
Με πρόσθεση λαμβάνουμε το ζητούμενο.
Από την απόδειξη αυτή φαίνεται ότι η διάταξη δεν παίζει κανέναν ρόλο, απλώς χρειάζεται να είναι
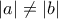 ή
ή 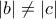 ή
ή 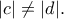
Με ανάλογο τρόπο αποδεικνύεται και η δεύτερη.
Μάγκος Θάνος
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες
