

Να αποδείξετε ότι οι
 είναι κορυφές ισοσκελούς τριγώνου στο μιγαδικό επίπεδο.
είναι κορυφές ισοσκελούς τριγώνου στο μιγαδικό επίπεδο.Συντονιστής: chris_gatos


 είναι κορυφές ισοσκελούς τριγώνου στο μιγαδικό επίπεδο.
είναι κορυφές ισοσκελούς τριγώνου στο μιγαδικό επίπεδο. ,
,  ,
, 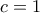 , τότε η συνθήκη ικανοποιείται, αλλά το τρίγωνο που σχηματίζεται δεν είναι ισόπλευρο (γεωμετρικά).
, τότε η συνθήκη ικανοποιείται, αλλά το τρίγωνο που σχηματίζεται δεν είναι ισόπλευρο (γεωμετρικά).Ισοσκελες γράφει και όχι ισόπλευρο, αλλά και πάλι δεν ισχύει, θεωρώντας για παράδειγμα εκφυλισμενο Ισοσκελες τρίγωνο με μία κορυφή στο
 και δύο κορυφές στο
και δύο κορυφές στο 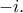
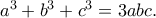
Έχουμεchris_gatos έγραψε: ↑Δευ Ιαν 29, 2024 6:00 pmΈστω τρεις μιγαδικοί αριθμοί για τους οποίους ισχύει:
Να αποδείξετε ότι οιείναι κορυφές ισοσκελούς τριγώνου στο μιγαδικό επίπεδο.
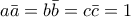 οπότε
οπότε 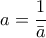 και όμοια τα άλλα δύο. Άρα
και όμοια τα άλλα δύο. Άρα 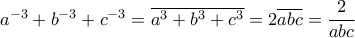 .
.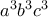 έχουμε
έχουμε 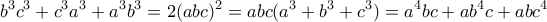 και άρα
και άρα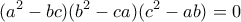
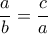 και κυκλικά. Άρα (αν ισχύει το πρώτα αλλά όμοια για τα άλλα) η γωνία που σχηματίζουν τα
και κυκλικά. Άρα (αν ισχύει το πρώτα αλλά όμοια για τα άλλα) η γωνία που σχηματίζουν τα  είναι ίση με την γωνία που σχηματίζουν τα
είναι ίση με την γωνία που σχηματίζουν τα  , όπως θέλαμε.
, όπως θέλαμε.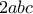 στην
στην 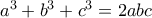 μπορούμε να βάλουμε το
μπορούμε να βάλουμε το  ή το
ή το 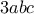 . Η απόδειξη δεν αλλάζει ουσιαστικά
. Η απόδειξη δεν αλλάζει ουσιαστικά  πρέπει να βρίσκονται στον μοναδιαίο κύκλο,
πρέπει να βρίσκονται στον μοναδιαίο κύκλο, 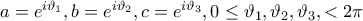
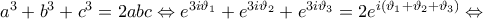
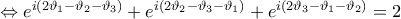
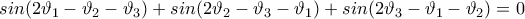
 , τότε εύκολα δείχνουμε πως:
, τότε εύκολα δείχνουμε πως: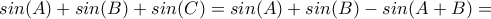

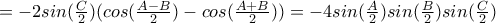
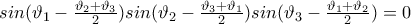
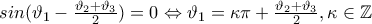
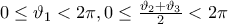
 αρκεί να ισχύει:
αρκεί να ισχύει: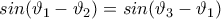 (*)
(*) :
:
 :
: 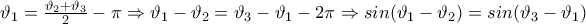
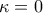 :
: 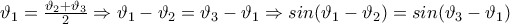
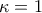 :
: 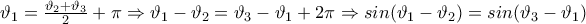
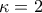 : θα πρέπει αναγκαστικά
: θα πρέπει αναγκαστικά 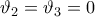 , που είναι άτοπο.
, που είναι άτοπο. στην δεύτερη συνθήκη μπορεί να είναι τυχαία, αφού το ίδιο θα έβγαινε και αν η συνθήκη ήταν η:
στην δεύτερη συνθήκη μπορεί να είναι τυχαία, αφού το ίδιο θα έβγαινε και αν η συνθήκη ήταν η: 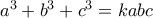 , με
, με  να περιορίζεται πιθανώς στο
να περιορίζεται πιθανώς στο ![[-3,3] [-3,3]](/forum/ext/geomar/texintegr/latexrender/pictures/083d33f8040330c3051e16ce69a5b0df.png) .
. 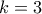 εύκολα προκύπτει πως το τρίγωνο θα είναι ισόπλευρο.
εύκολα προκύπτει πως το τρίγωνο θα είναι ισόπλευρο.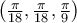 ,
, 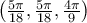 ,
, 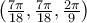 .
.Μιχάλη εύγε. Πολύ ωραία λύση. "Πολυωνυμική".Mihalis_Lambrou έγραψε: ↑Τρί Ιαν 30, 2024 10:53 pmΈχουμεchris_gatos έγραψε: ↑Δευ Ιαν 29, 2024 6:00 pmΈστω τρεις μιγαδικοί αριθμοί για τους οποίους ισχύει:
Να αποδείξετε ότι οιείναι κορυφές ισοσκελούς τριγώνου στο μιγαδικό επίπεδο.
οπότε
και όμοια τα άλλα δύο. Άρα
.
Πολλαπλάσιάζοντας επίέχουμε
και άρα
Άρακαι κυκλικά. Άρα (αν ισχύει το πρώτα αλλά όμοια για τα άλλα) η γωνία που σχηματίζουν τα
είναι ίση με την γωνία που σχηματίζουν τα
, όπως θέλαμε.
Σχόλιο: Μπορεί το τρίγωνο να είναι εκφυλισμένο.
Edit αργότερα: Το ενδιαφέρον είναι ότι στην θέση τουστην
μπορούμε να βάλουμε το
ή το
. Η απόδειξη δεν αλλάζει ουσιαστικά
Βεβαίως η άσκηση ζητούσε να αποδείξουμε ότι αν ισχύει η σχέση το τρίγωνο είναι ισοσκελές, όχι το αντίστροφο -- πράγματι υπάρχει αφθονία ισοσκελών τριγώνων όπου η σχέση δεν ισχύει, πχ
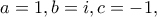 οπότε
οπότε 
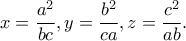
 (μετά από διαίρεση της δοσμένης σχέσης με
(μετά από διαίρεση της δοσμένης σχέσης με  )
)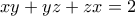 (μετά από διαίρεση της σχέσης
(μετά από διαίρεση της σχέσης 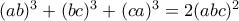 , από το ποστ του κυρίου Λάμπρου, με
, από το ποστ του κυρίου Λάμπρου, με 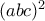 )
)
 ρίζες του πολυωνύμου
ρίζες του πολυωνύμου  .
. ρίζα, οπότε
ρίζα, οπότε 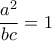 ή
ή 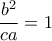 ή
ή 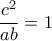 και παίρνουμε το ισοσκελές τρίγωνο με το επιχείρημα του κυρίου Λάμπρου για τις γωνίες (στο τέλος του αντίστοιχου ποστ).
και παίρνουμε το ισοσκελές τρίγωνο με το επιχείρημα του κυρίου Λάμπρου για τις γωνίες (στο τέλος του αντίστοιχου ποστ). , αλλά αυτό δε ζητείται στην εκφώνηση.
, αλλά αυτό δε ζητείται στην εκφώνηση.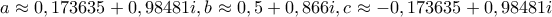
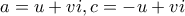 και επιλέγοντας
και επιλέγοντας 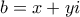 με
με  (μη ισοσκελές τρίγωνο), προκύπτει λόγω των
(μη ισοσκελές τρίγωνο), προκύπτει λόγω των 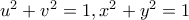 η ισοδυναμία της
η ισοδυναμία της 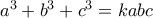 προς τις
προς τις 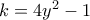 και
και 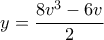 ... οπότε για
... οπότε για  προκύπτει
προκύπτει 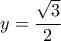 (ή η αρνητική της) και
(ή η αρνητική της) και 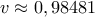 (και δύο ακόμη πιθανώς αποδεκτές λύσεις που δεν έλεγξα) κλπ
(και δύο ακόμη πιθανώς αποδεκτές λύσεις που δεν έλεγξα) κλπ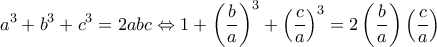
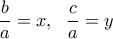
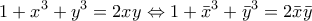
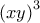 και με δεδομένο ότι
και με δεδομένο ότι 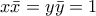
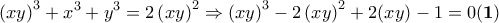
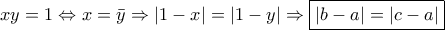
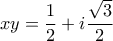 (κυβική ρίζα του -1) οπότε
(κυβική ρίζα του -1) οπότε 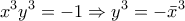 και από την
και από την 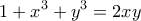 έχουμε:
έχουμε: 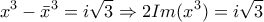
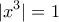 και έτσι
και έτσι 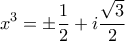 και
και 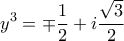
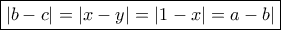 ή
ή 
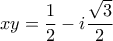 ομοίως....
ομοίως....

Κανένα λάθος, απλώς το τρίγωνο είναι ισοσκελες στο Α αντί του Βgbaloglou έγραψε: ↑Τετ Ιαν 31, 2024 1:53 pmΑντί λύσης (που νόμιζα πως είχα) ... μου προέκυψε αντιπαράδειγμα:

Γενικότερα, αρχίζοντας μεκαι επιλέγοντας
με
(μη ισοσκελές τρίγωνο), προκύπτει λόγω των
η ισοδυναμία της
προς τις
και
... οπότε για
προκύπτει
(ή η αρνητική της) και
(και δύο ακόμη πιθανώς αποδεκτές λύσεις που δεν έλεγξα) κλπ
Τι συμβαίνει; Έχω κάνει κάποιο λάθος κάπου; Επισυνάπτω τους υπολογισμούς του λογισμικού που επαληθεύουν το παράδειγμα μου (νομίζω)
three-cubes-and-a-double-product.png
Χρήστο, όταν γράφεις τρία τρίγωνα, προφανώς, εννοείς τρία ως προς το μέτρο των γωνιών τους. Οι τριάδες των μιγαδικώνchris_gatos έγραψε: ↑Τρί Ιαν 30, 2024 11:06 pm
Για το συγκεκριμένο βγαίνουν τρία τρίγωνα.
Αυτά με γωνίες,
,
.
 είναι πολλές....
είναι πολλές.... 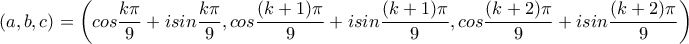 με
με 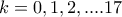


Η στρατηγική μου (#11) ήταν να περιοριστώ σε τρίγωνα με μία πλευρά παράλληλη προς τον άξονα τωνabgd έγραψε: ↑Τετ Ιαν 31, 2024 8:40 pmΧρήστο, όταν γράφεις τρία τρίγωνα, προφανώς, εννοείς τρία ως προς το μέτρο των γωνιών τους. Οι τριάδες των μιγαδικώνchris_gatos έγραψε: ↑Τρί Ιαν 30, 2024 11:06 pm
Για το συγκεκριμένο βγαίνουν τρία τρίγωνα.
Αυτά με γωνίες,
,
.
είναι πολλές....
με
Υπάρχουν κι άλλες...
 , καθώς ο πολλαπλασιασμός των
, καθώς ο πολλαπλασιασμός των  επί τυχόντα μιγαδικό
επί τυχόντα μιγαδικό  μέτρου
μέτρου  αφ' ενός μεν διατηρεί την
αφ' ενός μεν διατηρεί την 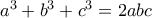 (πολλαπλασιάζοντας αμφότερα τα μέλη επί
(πολλαπλασιάζοντας αμφότερα τα μέλη επί 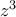 ), αφ' ετέρου δε αντιστοιχεί σε στροφή του τριγώνου (καλύπτοντας τελικά όλα τα τρίγωνα με την εν λόγω ιδιότητα). Έτσι άρχισα (#11) με
), αφ' ετέρου δε αντιστοιχεί σε στροφή του τριγώνου (καλύπτοντας τελικά όλα τα τρίγωνα με την εν λόγω ιδιότητα). Έτσι άρχισα (#11) με 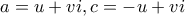 ... και θα συνεχίσω εκεί
... και θα συνεχίσω εκεί Δεν είναι αντιπαράδειγμα, όπως είπαμε (#13), απλώς τρίγωνο ισοσκελές στο A αντί του 'αναμενόμενου' B. Για να πάμε και στις άλλες λύσεις (με x\neq 0), έξι συνολικά της 8v^3-6v=\pm \sqrt{3}, και στα αντίστοιχα δώδεκα ισοσκελή τρίγωνα (με πρώτη την κορυφή του ισοσκελούς και με το A πάντα στα δεξιά):gbaloglou έγραψε: ↑ Αντί λύσης (που νόμιζα πως είχα) ... μου προέκυψε αντιπαράδειγμα: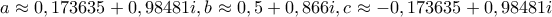
Γενικότερα, αρχίζοντας μεκαι επιλέγοντας
με
(μη ισοσκελές τρίγωνο), προκύπτει λόγω των
η ισοδυναμία της
προς τις
και
... οπότε για
προκύπτει
(ή η αρνητική της) και
(και δύο ακόμη πιθανώς αποδεκτές λύσεις που δεν έλεγξα) κλπ
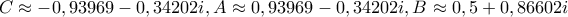
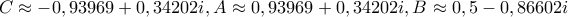
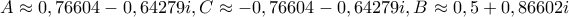
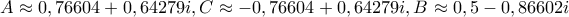
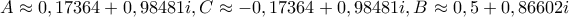
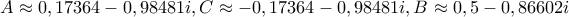
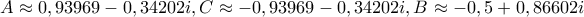
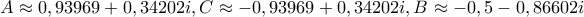
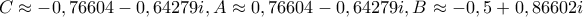
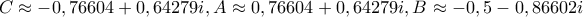
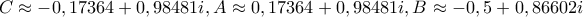
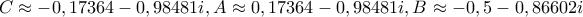
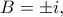 όπου προκύπτουν έξι (ουσιαστικά τρία) ισοσκελή τρίγωνα από τις έξι λύσεις της
όπου προκύπτουν έξι (ουσιαστικά τρία) ισοσκελή τρίγωνα από τις έξι λύσεις της 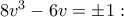
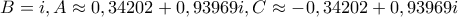
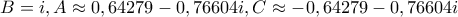
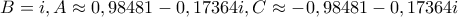
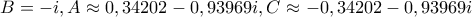
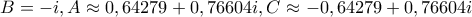
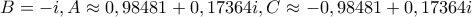
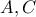 και τρία ουσιαστικά 'ορθά' κορυφής
και τρία ουσιαστικά 'ορθά' κορυφής  ) είναι, πιστεύω, όλα τα επί του μοναδιαίου κύκλου τρίγωνα κορυφών
) είναι, πιστεύω, όλα τα επί του μοναδιαίου κύκλου τρίγωνα κορυφών  που ικανοποιούν την
που ικανοποιούν την 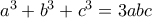 με μία πλευρά παράλληλη προς τον άξονα των
με μία πλευρά παράλληλη προς τον άξονα των  (πλευρά ισοσκελούς τριγώνου στις πρώτες τρεις περιπτώσεις, βάση ισοσκελούς τριγώνου στις τελευταίες τρεις περιπτώσεις).
(πλευρά ισοσκελούς τριγώνου στις πρώτες τρεις περιπτώσεις, βάση ισοσκελούς τριγώνου στις τελευταίες τρεις περιπτώσεις).Χρήστο πως κατέληξες στα τρία τρίγωνα; Ναι, είναι αυτά στα οποία κατέληξα και εγώ, εμπειρικά όμως, χωρίς καν να έχω αποδείξει ότι είναι ισοσκελη. Αν γνωρίζω ότι ουσιαστικά υπάρχουν τρία ακριβώς τρίγωνα που ικανοποιούν την δοθείσα συνθήκη και ότι αυτά είναι ισοσκελη, τότε ναι, μπορώ να περιοριστώ στην περίπτωσηchris_gatos έγραψε: ↑Τρί Ιαν 30, 2024 11:06 pmΚαλησπέρα Σωτήρη. Γιώργο, Σιλουανέ!
Σας ευχαριστώ θερμά για την ανασχόληση. Από χτες κατάλαβα από μηνύματα φίλων πως υπάρχει σύγχυση με γνωστή άσκηση
στην οποία στο δεύτερο μέλος υπάρχει τρία και αναφέρεται σε ισόπλευρο τρίγωνο ενώ αυτή σε ισοσκελές.
Παράληψη μου είναι πως δεν ανέφερα πως δεν πιάνεται περίπτωση εκφυλισμένου τριγώνου.
Η λύση που διαθέτω αποδεικνύει πως μπορώ να βάλω στη θέση του δύο οποιονδήποτε αριθμό από το πλήν ένα έως και το τρια και να λάβω λύση.
Για το συγκεκριμένο βγαίνουν τρία τρίγωνα.
Αυτά με γωνίες,
,
.
Nu
Μόλις βρω χρόνο θα ανεβάσω μια λύση.
Καλό σας βράδυ και ευχαριστώ ξανά για το ενδιαφέρον!
Edit:
Όσο έγραφα ο Μιχάλης και ο Γρηγόρης έδωσαν τις σκέψεις τους. Τους ευχαριστώ πολύ και αυτούς.
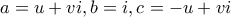 - - ή διαπραγμάτευση μου εξηγεί πως - - και να καταλήξω στην συνθήκη
- - ή διαπραγμάτευση μου εξηγεί πως - - και να καταλήξω στην συνθήκη 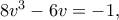 και επίσης από νόμο συνημιτονων στο ισοσκελες βγάζω για την γωνία κορυφής
και επίσης από νόμο συνημιτονων στο ισοσκελες βγάζω για την γωνία κορυφής 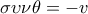 , οπότε
, οπότε 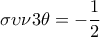 και εύκολα οι τρεις ρίζες της τριτοβάθμιας οδηγούν στις τρεις γωνίες κορυφής,
και εύκολα οι τρεις ρίζες της τριτοβάθμιας οδηγούν στις τρεις γωνίες κορυφής, 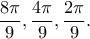
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες