 ένα σημείο στο εσωτερικό ενός ισοπλεύρου τριγώνου
ένα σημείο στο εσωτερικό ενός ισοπλεύρου τριγώνου 
πλευράς
 .
. Αν οι
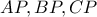 τέμνουν αντίστοιχα τις πλευρές
τέμνουν αντίστοιχα τις πλευρές  στα σημεία
στα σημεία 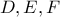
τότε να αποδείξετε ότι:

Συντονιστής: chris_gatos
 ένα σημείο στο εσωτερικό ενός ισοπλεύρου τριγώνου
ένα σημείο στο εσωτερικό ενός ισοπλεύρου τριγώνου 
 .
. 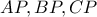 τέμνουν αντίστοιχα τις πλευρές
τέμνουν αντίστοιχα τις πλευρές  στα σημεία
στα σημεία 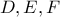

Παρατηρούμε για τις Σεβιανέςchris_gatos έγραψε: ↑Δευ Αύγ 21, 2023 1:09 pmΈστωένα σημείο στο εσωτερικό ενός ισοπλεύρου τριγώνου
πλευράς
. Αν οι
τέμνουν αντίστοιχα τις πλευρές
στα σημεία
τότε να αποδείξετε ότι:

 που διέρχονται από το
που διέρχονται από το  ότι:
ότι:  χωρίς οι
χωρίς οι  να ισχύουν όλες ταυτόχρονα.
να ισχύουν όλες ταυτόχρονα. 
 είναι γνωστή πρόταση που αφορά σε Σεβιανές που διέρχονται από κοινό μη εξωτερικό σημείο σε τυχόν τρίγωνο, και ενας τρόπος απόδειξης είναι με χρήση του βασικού τύπου του εμβαδού τριγώνου (συγκεκριμένα και τελικά για την απόδειξη χρησιμοποιούμε ότι ο λόγος των εμβαδών δύο τριγώνων ίδιας βάσης ισούται με τον λόγο των αντίστοιχων υψών τους).
είναι γνωστή πρόταση που αφορά σε Σεβιανές που διέρχονται από κοινό μη εξωτερικό σημείο σε τυχόν τρίγωνο, και ενας τρόπος απόδειξης είναι με χρήση του βασικού τύπου του εμβαδού τριγώνου (συγκεκριμένα και τελικά για την απόδειξη χρησιμοποιούμε ότι ο λόγος των εμβαδών δύο τριγώνων ίδιας βάσης ισούται με τον λόγο των αντίστοιχων υψών τους). οι προβολές των
οι προβολές των  στην
στην  . Έχουμε
. Έχουμε  και
και  . Άρα
. Άρα 
 και
και 
 και άρα
και άρα  .
.Φέρνωchris_gatos έγραψε: ↑Δευ Αύγ 21, 2023 1:09 pmΈστωένα σημείο στο εσωτερικό ενός ισοπλεύρου τριγώνου
πλευράς.
Αν οιτέμνουν αντίστοιχα τις πλευρές
στα σημεία
τότε να αποδείξετε ότι:

 όπως φαίνεται στο σχήμα.
Το
όπως φαίνεται στο σχήμα.
Το  είναι ισόπλευρο, άρα
είναι ισόπλευρο, άρα  Έχουμε λοιπόν:
Έχουμε λοιπόν:

 ένα σημείο στο εσωτερικό τριγώνου
ένα σημείο στο εσωτερικό τριγώνου  Αν οι
Αν οι 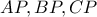 τέμνουν τις πλευρές
τέμνουν τις πλευρές  στα σημεία
στα σημεία 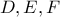 αντίστοιχα, τότε
αντίστοιχα, τότε 
Αν λάβουμε υπόψη ότι η μεγαλύτερη από τρεις Σεβιανές είναι μικρότερη ή ίση από τοgeorge visvikis έγραψε: ↑Τρί Αύγ 22, 2023 6:45 pmΓΕΝΙΚΕΥΣΗ: Έστωένα σημείο στο εσωτερικό τριγώνου
Αν οι
τέμνουν τις πλευρές
στα σημεία
αντίστοιχα, τότε

 , μπορούμε να εφαρμόσουμε την ίδια ακριβώς ημέτερη μέθοδο επίλυσης που ανέπτυξα πιο πάνω.
, μπορούμε να εφαρμόσουμε την ίδια ακριβώς ημέτερη μέθοδο επίλυσης που ανέπτυξα πιο πάνω.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες