 είναι μία κορυφή ενός τετραγώνου του οποίου η μία πλευρά βρίσκεται στην ευθεία
είναι μία κορυφή ενός τετραγώνου του οποίου η μία πλευρά βρίσκεται στην ευθεία  . Να υπολογιστεί το εμβαδόν του και οι κορυφές του.
. Να υπολογιστεί το εμβαδόν του και οι κορυφές του.Συντονιστής: Τηλέγραφος Κώστας
 είναι μία κορυφή ενός τετραγώνου του οποίου η μία πλευρά βρίσκεται στην ευθεία
είναι μία κορυφή ενός τετραγώνου του οποίου η μία πλευρά βρίσκεται στην ευθεία  . Να υπολογιστεί το εμβαδόν του και οι κορυφές του.
. Να υπολογιστεί το εμβαδόν του και οι κορυφές του.
α) Το εμβαδόν καθενός από τα δύο τετράγωνα είναι ίσο με το τετράγωνο της απόστασης τουTolaso J Kos έγραψε: ↑Κυρ Μαρ 24, 2024 9:35 amΤο σημείοείναι μία κορυφή ενός τετραγώνου του οποίου η μία πλευρά βρίσκεται στην ευθεία
. Να υπολογιστεί το εμβαδόν του και οι κορυφές του.
 από την
από την 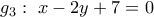 .
.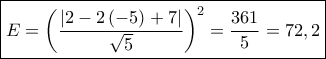 .
.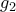 παράλληλη στην
παράλληλη στην 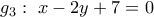 έχει γενική εξίσωση,
έχει γενική εξίσωση,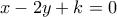 και ως διερχομένη από το
και ως διερχομένη από το 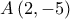
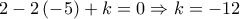 , δηλαδή
, δηλαδή 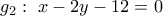 .
.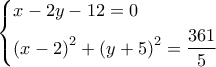 προκύπτουν τα ,
προκύπτουν τα , 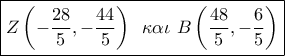 .
Από τη λύση του συστήματος ,
.
Από τη λύση του συστήματος , 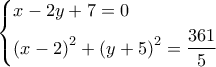 προκύπτει, μοναδική λύση ,
προκύπτει, μοναδική λύση ,  ( επαφή κύκλου κι ευθείας).
( επαφή κύκλου κι ευθείας).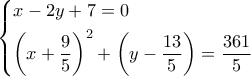 , προκύπτουν τα ,
, προκύπτουν τα , 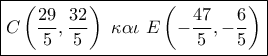 .
.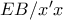 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 12 επισκέπτες