 και η έλλειψη
και η έλλειψη  .
.- Να δειχθεί ότι οι εφαπτόμενες που φέρονται απ' τις εστίες της έλλειψης προς τον κύκλο σχηματίζουν ρόμβο.
- Αν
 το εμβαδόν του του παραπάνω ρόμβου και
το εμβαδόν του του παραπάνω ρόμβου και  το εμβαδόν που σχηματίζεται απ' τα σημεία επαφής, να δειχθεί ότι
το εμβαδόν που σχηματίζεται απ' τα σημεία επαφής, να δειχθεί ότι  .
.
Συντονιστής: Τηλέγραφος Κώστας
 και η έλλειψη
και η έλλειψη  .
. το εμβαδόν του του παραπάνω ρόμβου και
το εμβαδόν του του παραπάνω ρόμβου και  το εμβαδόν που σχηματίζεται απ' τα σημεία επαφής, να δειχθεί ότι
το εμβαδόν που σχηματίζεται απ' τα σημεία επαφής, να δειχθεί ότι  .
.

 , όπου
, όπου  η εξίσωση της έλλειψης. Σε αυτή την περίπτωση
η εξίσωση της έλλειψης. Σε αυτή την περίπτωση  και
και  , άρα
, άρα 
 και
και  , αφού το κέντρο της έλλειψης είναι το
, αφού το κέντρο της έλλειψης είναι το  . Επειδή τυγχαίνει και το κέντρο του κύκλου να είναι το ίδιο, οι εστίες έχουν την ίδια απόσταση και απο το κέντρο του κύκλου. Έτσι μπορούμε να βρουμε τις εφαπτομένες που φέρονται από τις εστίες στον κύκλο. Οι ευθείες αυτές βρίσκονται με τον τύπο
. Επειδή τυγχαίνει και το κέντρο του κύκλου να είναι το ίδιο, οι εστίες έχουν την ίδια απόσταση και απο το κέντρο του κύκλου. Έτσι μπορούμε να βρουμε τις εφαπτομένες που φέρονται από τις εστίες στον κύκλο. Οι ευθείες αυτές βρίσκονται με τον τύπο  , όπου f η απόσταση του σημείου απο τον κύκλο (σε αυτή την περίπτωση είναι
, όπου f η απόσταση του σημείου απο τον κύκλο (σε αυτή την περίπτωση είναι  ) και
) και  (Όλα αυτά όταν η ακτίνα του κύκλου ρ=1 και τα σημεία βρίσκονται στο ίδιο ύψος με το κέντρο του κύκλου). Άρα
(Όλα αυτά όταν η ακτίνα του κύκλου ρ=1 και τα σημεία βρίσκονται στο ίδιο ύψος με το κέντρο του κύκλου). Άρα  , και οι τέσσερις εφαπτομένες είναι οι εξής:
, και οι τέσσερις εφαπτομένες είναι οι εξής:






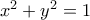 . Η λύση των συγκεκριμένων είναι τα
. Η λύση των συγκεκριμένων είναι τα  .
. και πράγματι ισχύει πως
και πράγματι ισχύει πως
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης