Ορθοκεντρικό τετράεδρο
Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
- Al.Koutsouridis
- Δημοσιεύσεις: 1816
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Ορθοκεντρικό τετράεδρο
Ορισμός Το τετράεδρο, στο οποίο τα τέσσερα ύψη του διέρχονται από το ίδιο σημείο, ονομάζεται ορθοκεντρικό τετράεδρο και το σημείο τομής των υψών του ορθόκεντρο του τετράεδρου.
Να αποδείξετε τις παρακάτω ιδιότητες:
1. Ένα τετράεδρο είναι ορθοκεντρικό αν και μόνο αν οι κάθετες προς τις έδρες από τα κέντρα βάρους τοων εδρών του διέρχονται από το ίδιο σημείο.
2. Σε ορθοκεντρικό τετράεδρο και μόνο σε αυτό τα ζεύγη απέναντι ακμών του είναι κάθετα.
3. Σε ορθοκεντρικό τετράεδρο και μόνο σε αυτό οι βάσεις των υψών του είναι ορθόκεντρα των εδρών του.
4. Ένα τετράεδρο είναι ορθοκεντρικό αν και μόνο αν το άθροισμα των τετραγώνων των μηκών απέναντι ακμών του είναι ίσα μεταξύ τους.
5. Σε ένα ορθοκεντρικό τετράεδρο και μόνο σε αυτό τα γινόμενα των συνημιτόνων των διέδρων γωνιών που αντιστοιχούν σε απέναντι ακμές είναι ίσα μεταξύ τους.
6. Ικανή και αναγκαία συνθήκη να είναι ένα τετράεδρο ορθοκεντρικό, είναι το μήκος των τμημάτων που ενώνουν τα μέσα απέναντι ακμών του (διδιάμεσος), να είναι ίσα μεταξύ τους.
Να αποδείξετε τις παρακάτω ιδιότητες:
1. Ένα τετράεδρο είναι ορθοκεντρικό αν και μόνο αν οι κάθετες προς τις έδρες από τα κέντρα βάρους τοων εδρών του διέρχονται από το ίδιο σημείο.
2. Σε ορθοκεντρικό τετράεδρο και μόνο σε αυτό τα ζεύγη απέναντι ακμών του είναι κάθετα.
3. Σε ορθοκεντρικό τετράεδρο και μόνο σε αυτό οι βάσεις των υψών του είναι ορθόκεντρα των εδρών του.
4. Ένα τετράεδρο είναι ορθοκεντρικό αν και μόνο αν το άθροισμα των τετραγώνων των μηκών απέναντι ακμών του είναι ίσα μεταξύ τους.
5. Σε ένα ορθοκεντρικό τετράεδρο και μόνο σε αυτό τα γινόμενα των συνημιτόνων των διέδρων γωνιών που αντιστοιχούν σε απέναντι ακμές είναι ίσα μεταξύ τους.
6. Ικανή και αναγκαία συνθήκη να είναι ένα τετράεδρο ορθοκεντρικό, είναι το μήκος των τμημάτων που ενώνουν τα μέσα απέναντι ακμών του (διδιάμεσος), να είναι ίσα μεταξύ τους.
Λέξεις Κλειδιά:
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13344
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: Ορθοκεντρικό τετράεδρο
Στην ελληνική βιβλιογραφία η ιδιότητα (2) είναι ο ορισμός του ορθοκεντρικού τετραέδρου, ενώ τα τρία ύψη που διέρχονται από το ίδιο σημείο αποτελεί ιδιότητα και χρειάζεται απόδειξη.
Έστω  δύο από τα ύψη του τετραέδρου. Οι ευθείες
δύο από τα ύψη του τετραέδρου. Οι ευθείες  είναι ορθογώνιες της
είναι ορθογώνιες της 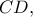 οπότε τα επίπεδα
οπότε τα επίπεδα  θα είναι κάθετα στη
θα είναι κάθετα στη  Επειδή όμως τα επίπεδα αυτά έχουν κοινή την
Επειδή όμως τα επίπεδα αυτά έχουν κοινή την  θα ταυτίζονται. Έτσι, τα
θα ταυτίζονται. Έτσι, τα  είναι ομοεπίπεδα. Δεν μπορεί όμως να είναι παράλληλα γιατί είναι κάθετα σε τεμνόμενα επίπεδα, άρα τέμνονται σε ένα σημείο
είναι ομοεπίπεδα. Δεν μπορεί όμως να είναι παράλληλα γιατί είναι κάθετα σε τεμνόμενα επίπεδα, άρα τέμνονται σε ένα σημείο  Αποδείξαμε λοιπόν ότι τα ύψη του τετραέδρου τέμνονται ανά δύο κι επειδή δεν βρίσκονται στο ίδιο επίπεδο, θα διέρχονται αναγκαστικά από το ίδιο σημείο
Αποδείξαμε λοιπόν ότι τα ύψη του τετραέδρου τέμνονται ανά δύο κι επειδή δεν βρίσκονται στο ίδιο επίπεδο, θα διέρχονται αναγκαστικά από το ίδιο σημείο  που ονομάζεται ορθόκεντρο του τετραέδρου.
που ονομάζεται ορθόκεντρο του τετραέδρου.
 δύο από τα ύψη του τετραέδρου. Οι ευθείες
δύο από τα ύψη του τετραέδρου. Οι ευθείες  είναι ορθογώνιες της
είναι ορθογώνιες της 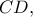 οπότε τα επίπεδα
οπότε τα επίπεδα  θα είναι κάθετα στη
θα είναι κάθετα στη  Επειδή όμως τα επίπεδα αυτά έχουν κοινή την
Επειδή όμως τα επίπεδα αυτά έχουν κοινή την  θα ταυτίζονται. Έτσι, τα
θα ταυτίζονται. Έτσι, τα  είναι ομοεπίπεδα. Δεν μπορεί όμως να είναι παράλληλα γιατί είναι κάθετα σε τεμνόμενα επίπεδα, άρα τέμνονται σε ένα σημείο
είναι ομοεπίπεδα. Δεν μπορεί όμως να είναι παράλληλα γιατί είναι κάθετα σε τεμνόμενα επίπεδα, άρα τέμνονται σε ένα σημείο  Αποδείξαμε λοιπόν ότι τα ύψη του τετραέδρου τέμνονται ανά δύο κι επειδή δεν βρίσκονται στο ίδιο επίπεδο, θα διέρχονται αναγκαστικά από το ίδιο σημείο
Αποδείξαμε λοιπόν ότι τα ύψη του τετραέδρου τέμνονται ανά δύο κι επειδή δεν βρίσκονται στο ίδιο επίπεδο, θα διέρχονται αναγκαστικά από το ίδιο σημείο  που ονομάζεται ορθόκεντρο του τετραέδρου.
που ονομάζεται ορθόκεντρο του τετραέδρου.
τελευταία επεξεργασία από george visvikis σε Παρ Μαρ 01, 2024 11:26 pm, έχει επεξεργασθεί 1 φορά συνολικά.
- Al.Koutsouridis
- Δημοσιεύσεις: 1816
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Re: Ορθοκεντρικό τετράεδρο
Καλησπέρα κ. Γιώργο καλά κάνατε και το αναφέρατε σε περίπτωση, που θέλουν να το ψάξουν παραπέρα οι μαθητές. Εγώ διάλεξα αυτόν, γιατί αποδίδει καλύτερα τον όρο ορθοκεντρικό. Τα τετράεδρα με αυτήν την ιδίοτητα αναφέρονται και ως ορθογώνια, σε τέτοια περίπτωση, αν τα ονομάσουμε ορθογώνια , ταιριάζει πιο πολύ ο ορισμός της ελληνικής βιβλιογραφίας. Βέβαια το σημαντικό εδώ, είναι η ισοδυναμία των ορισμών και ιδιοτήτων.george visvikis έγραψε: ↑Παρ Μαρ 01, 2024 2:56 pmΣτην ελληνική βιβλιογραφία η ιδιότητα (2) είναι ο ορισμός του ορθοκεντρικού τετραέδρου, ενώ τα τρία ύψη που διέρχονται από το ίδιο σημείο αποτελεί ιδιότητα και χρειάζεται απόδειξη.
-
ΚΕΦΑΛΟΝΙΤΗΣ
- Δημοσιεύσεις: 1294
- Εγγραφή: Δευ Δεκ 28, 2009 11:41 pm
- Τοποθεσία: Kάπου στο πιο μεγάλο νησί του Ιονίου
Re: Ορθοκεντρικό τετράεδρο
Ανεξάρτητα από ποιον ορισμό επιλέγει κάποιος, ο Αλέξανδρος μας έδωσε αρκετό υλικό για ψάξιμο.
Εγώ τουλάχιστον το εκτιμώ αυτό.
Εγώ τουλάχιστον το εκτιμώ αυτό.
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13344
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: Ορθοκεντρικό τετράεδρο
Al.Koutsouridis έγραψε: ↑Παρ Μαρ 01, 2024 1:40 pmΟρισμός Το τετράεδρο, στο οποίο τα τέσσερα ύψη του διέρχονται από το ίδιο σημείο, ονομάζεται ορθοκεντρικό τετράεδρο και το σημείο τομής των υψών του ορθόκεντρο του τετράεδρου.
Να αποδείξετε τις παρακάτω ιδιότητες:
1. Ένα τετράεδρο είναι ορθοκεντρικό αν και μόνο αν οι κάθετες προς τις έδρες από τα κέντρα βάρους τοων εδρών του διέρχονται από το ίδιο σημείο.
2. Σε ορθοκεντρικό τετράεδρο και μόνο σε αυτό τα ζεύγη απέναντι ακμών του είναι κάθετα.
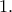 Έστω
Έστω  το κέντρο βάρους της έδρας
το κέντρο βάρους της έδρας  του ορθοκεντρικού τετραέδρου
του ορθοκεντρικού τετραέδρου  και
και  κάθετη
κάθετη στην έδρα αυτή. Έστω ακόμα
 το ύψος,
το ύψος,  το ορθόκεντρο και
το ορθόκεντρο και  το βαρύκεντρο του τετραέδρου.
Ως γνωστόν το
το βαρύκεντρο του τετραέδρου.
Ως γνωστόν το  είναι σημείο του τμήματος
είναι σημείο του τμήματος  και
και  Εξάλλου,
Εξάλλου,  οπότε η
οπότε η 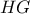 τέμνει την
τέμνει την 
σε ένα σημείο έστω
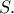 Τότε
Τότε  και αφού τα σημεία
και αφού τα σημεία  είναι σταθερά και το
είναι σταθερά και το  θα είναι σταθερό.
θα είναι σταθερό. Ομοίως το ίδιο θα συμβαίνει και για τις άλλες έδρες.
Αντίστροφα, αν οι κάθετες στις έδρες από τα κέντρα βάρους αυτών διέρχονται από το ίδιο σημείο
 και η
και η  τέμνει το
τέμνει το ύψος
 στο
στο  τότε
τότε  άρα το
άρα το  είναι σταθερό σημείο του
είναι σταθερό σημείο του  . Ομοίως, το ίδιο συμβαίνει και
. Ομοίως, το ίδιο συμβαίνει και για τα άλλα ύψη, οπότε το τετράεδρο είναι ορθοκεντρικό.
 Στο σχήμα της πρώτης μου ανάρτησης (#2), αν τα ύψη
Στο σχήμα της πρώτης μου ανάρτησης (#2), αν τα ύψη  τέμνονται τότε η
τέμνονται τότε η  θα είναι κάθετη στο επίπεδό τους, άρα ορθογώνια της
θα είναι κάθετη στο επίπεδό τους, άρα ορθογώνια της  Ομοίως και οι άλλες απέναντι έδρες θα είναι ορθογώνιες. Το αντίστροφο αποδείχτηκε στην (#2).
Ομοίως και οι άλλες απέναντι έδρες θα είναι ορθογώνιες. Το αντίστροφο αποδείχτηκε στην (#2).Θα επανέλθω και για τα υπόλοιπα, αν δεν έχουν απαντηθεί μέχρι τότε.
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13344
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: Ορθοκεντρικό τετράεδρο
Al.Koutsouridis έγραψε: ↑Παρ Μαρ 01, 2024 1:40 pmΟρισμός Το τετράεδρο, στο οποίο τα τέσσερα ύψη του διέρχονται από το ίδιο σημείο, ονομάζεται ορθοκεντρικό τετράεδρο και το σημείο τομής των υψών του ορθόκεντρο του τετράεδρου.
Να αποδείξετε τις παρακάτω ιδιότητες:
3. Σε ορθοκεντρικό τετράεδρο και μόνο σε αυτό οι βάσεις των υψών του είναι ορθόκεντρα των εδρών του.
4. Ένα τετράεδρο είναι ορθοκεντρικό αν και μόνο αν το άθροισμα των τετραγώνων των μηκών απέναντι ακμών του είναι ίσα μεταξύ τους.
 Έστω
Έστω  ύψος του τετραέδρου. H
ύψος του τετραέδρου. H  είναι ορθογώνια της
είναι ορθογώνια της  και της
και της  άρα θα είναι κάθετη στο επίπεδο
άρα θα είναι κάθετη στο επίπεδο  οπότε
οπότε  Ομοίως,
Ομοίως,  Επομένως το
Επομένως το  είναι ορθόκεντρο του
είναι ορθόκεντρο του 
Ακολουθώντας ακριβώς την αντίστροφη διαδικασία, αποδεικνύεται και το αντίστροφο της πρότασης.
 Γνωρίζουμε ότι τα τμήματα
Γνωρίζουμε ότι τα τμήματα  είναι ορθογώνια αν και μόνο αν:
είναι ορθογώνια αν και μόνο αν: (κριτήριο ορθογωνιότητας).
(κριτήριο ορθογωνιότητας).Ομοίως για τα ορθογώνια τμήματα
 είναι
είναι  και η πρόταση αποδείχτηκε.
και η πρόταση αποδείχτηκε.- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13344
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: Ορθοκεντρικό τετράεδρο
ΈστωAl.Koutsouridis έγραψε: ↑Παρ Μαρ 01, 2024 1:40 pmΟρισμός Το τετράεδρο, στο οποίο τα τέσσερα ύψη του διέρχονται από το ίδιο σημείο, ονομάζεται ορθοκεντρικό τετράεδρο και το σημείο τομής των υψών του ορθόκεντρο του τετράεδρου.
Να αποδείξετε τις παρακάτω ιδιότητες:
6. Ικανή και αναγκαία συνθήκη να είναι ένα τετράεδρο ορθοκεντρικό, είναι το μήκος των τμημάτων που ενώνουν τα μέσα απέναντι ακμών του (διδιάμεσος), να είναι ίσα μεταξύ τους.
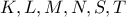 τα μέσα των ακμών τεραέδρου
τα μέσα των ακμών τεραέδρου  όπως φαίνονται στο σχήμα.
Τα
όπως φαίνονται στο σχήμα.
Τα  είναι παραλληλόγραμμα. Τα τμήματα
είναι παραλληλόγραμμα. Τα τμήματα  είναι ίσα, αν και μόνο αν τα παραλληλόγραμμα είναι ορθογώνια, δηλαδή αν και μόνο αν το τετράεδρο
είναι ίσα, αν και μόνο αν τα παραλληλόγραμμα είναι ορθογώνια, δηλαδή αν και μόνο αν το τετράεδρο  είναι ορθοκεντρικό.
είναι ορθοκεντρικό.Εκκρεμεί η (5) .
- Al.Koutsouridis
- Δημοσιεύσεις: 1816
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Re: Ορθοκεντρικό τετράεδρο
Να ευχαριστήσω τον κ.Γιώργο για τις λύσεις του και το χρόνο που διέθεσε. Νομίζω οι ιδιότητες μπορούν να χρησιμοποιηθούν για την λύση άλλων πιο σύνθετων θεμάτων για ορθοκεντρικά τετράεδρα, που έχουν εμφανιστεί στο
-
ΚΕΦΑΛΟΝΙΤΗΣ
- Δημοσιεύσεις: 1294
- Εγγραφή: Δευ Δεκ 28, 2009 11:41 pm
- Τοποθεσία: Kάπου στο πιο μεγάλο νησί του Ιονίου
Re: Ορθοκεντρικό τετράεδρο
Eπειδή πίσω από τους ορισμούς, τα θεωρήματα και τις ιδιότητες υπάρχουν άνθρωποι, μια μικρή αναφορά
σε αυτόν που πρωτομελέτησε και δημοσίευσε για το ορθοκεντρικό τετράεδρο.
Πρόκειται για τον Simon Lhuilier. Ο άνθρωπος αυτός προτίμησε να ασχοληθεί με τα μαθηματικά από νεαρή
ηλικία, μολονότι κάποιος συγγενής του πρότεινε να ακολουθήσει μια εκκλησιαστική καριέρα με αντάλλαγμα
μια μεγάλη περιουσία. Τα χρήματα δεν ήταν το παν για αυτόν...
Μια βιογραφία αυτού του ανθρώπου στον παρακάτω σύνδεσμο
https://mathshistory.st-andrews.ac.uk/B ... /Lhuilier/
σε αυτόν που πρωτομελέτησε και δημοσίευσε για το ορθοκεντρικό τετράεδρο.
Πρόκειται για τον Simon Lhuilier. Ο άνθρωπος αυτός προτίμησε να ασχοληθεί με τα μαθηματικά από νεαρή
ηλικία, μολονότι κάποιος συγγενής του πρότεινε να ακολουθήσει μια εκκλησιαστική καριέρα με αντάλλαγμα
μια μεγάλη περιουσία. Τα χρήματα δεν ήταν το παν για αυτόν...
Μια βιογραφία αυτού του ανθρώπου στον παρακάτω σύνδεσμο
https://mathshistory.st-andrews.ac.uk/B ... /Lhuilier/
- Al.Koutsouridis
- Δημοσιεύσεις: 1816
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Re: Ορθοκεντρικό τετράεδρο
ΈστωAl.Koutsouridis έγραψε: ↑Παρ Μαρ 01, 2024 1:40 pmΟρισμός Το τετράεδρο, στο οποίο τα τέσσερα ύψη του διέρχονται από το ίδιο σημείο, ονομάζεται ορθοκεντρικό τετράεδρο και το σημείο τομής των υψών του ορθόκεντρο του τετράεδρου.
Να αποδείξετε τις παρακάτω ιδιότητες:
5. Σε ένα ορθοκεντρικό τετράεδρο και μόνο σε αυτό τα γινόμενα των συνημιτόνων των διέδρων γωνιών που αντιστοιχούν σε απέναντι ακμές είναι ίσα μεταξύ τους.
 το δοθέν τετράεδρο και έστω
το δοθέν τετράεδρο και έστω  μοναδιαία διανύσματα, κάθετα στις έδρες
μοναδιαία διανύσματα, κάθετα στις έδρες  αντίστοιχα και με φορά εξωτερικά αυτού. Τότε τα διανύσματα
αντίστοιχα και με φορά εξωτερικά αυτού. Τότε τα διανύσματα  είναι συγραμμικό με το διάνυσμα
είναι συγραμμικό με το διάνυσμα  και το διάνυσμα
και το διάνυσμα  συγραμμικό με το
συγραμμικό με το  . Άρα
. Άρα
Όμως
 ,
,  και
και  ,
, 
(με
 συμβολίζουμε τα ημίτονα και συνημίτονα των διέδρων γωνιών στην ακμή
συμβολίζουμε τα ημίτονα και συνημίτονα των διέδρων γωνιών στην ακμή  )
)Οπότε

Εκφράσαμε δηλαδή το συνημίτονο της γωνίας δυο απέναντι ακμών ενός τετράεδρου συναρτήσει των ημιτόνων και συνημιτόνων των δίεδρων γωνιών του.
Στην περίπτωση του ορθοκεντρικού τετράεδρου είναι
 , οπότε
, οπότε  . Ομοίως και για τα άλλα ζεύγη απέναντι ακμών.
. Ομοίως και για τα άλλα ζεύγη απέναντι ακμών. Οι παραπάνω πράξεις είναι ισοδυναμίες οπότε ισχύει και το αντίστροφο.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Bing [Bot] και 10 επισκέπτες
