Ιερότητα τριγώνου

Γιώργος Μήτσιος · #1

Καλό μεσημέρι σε όλους.

: Ιερότητα τριγώνου.PNG (10.72 KiB) Προβλήθηκε 1154 φορές

Στο εσωτερικό του τριγώνου ABC

υπάρχει σημείο

ώστε να είναι $\widehat{ABH}=\widehat{ACH}=18^\circ$

ενώ

είναι το μέσον της

. Ο κύκλος με διάμετρο

τέμνει τις AB,AC

στα

και

αντιστοίχως.

Να εξεταστεί η ιερότητα του τριγώνου MNF

(Να βρεθούν τα μέτρα των γωνιών του). Σας ευχαριστώ, Γιώργος.

ΦΩΤΙΑΔΗΣ ΠΡΟΔΡΟΜΟΣ · #2

Γιώργος Μήτσιος έγραψε: ↑
Πέμ Φεβ 20, 2020 12:48 pm
Καλό μεσημέρι σε όλους.
Ιερότητα τριγώνου.PNG
Στο εσωτερικό του τριγώνου υπάρχει σημείο ώστε να είναι $\widehat{ABH}=\widehat{ACH}=18^\circ$

ενώ είναι το μέσον της . Ο κύκλος με διάμετρο τέμνει τις στα και αντιστοίχως.

Να εξεταστεί η ιερότητα του τριγώνου (Να βρεθούν τα μέτρα των γωνιών του). Σας ευχαριστώ, Γιώργος.

Ίσως κάτι δεν βλέπω.....

Λήμμα 1 :

: 233.PNG (31.26 KiB) Προβλήθηκε 1081 φορές

Έστω

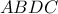τετράπλευρο εγγεγραμμένο σε κύκλο με A,D

αντιδιαμετρικά σημεία.Έστω K,L

στις ευθείες AB,AC

ώστε $\angle KDB=\angle LDC$ τότε αν

το μέσο του

θα είναι

Απόδειξη : Έστω X,Y

οι προβολές των K,L

στην

.Είναι $\dfrac{BX}{CY}=\dfrac{BK\cos\angle XBK}{CL\cos \angle YCL}=\dfrac{BD\tan\angle KDB\cos \angle CDA}{DC\tan \angle CDL\cos \angle ADB}=\dfrac{BD}{\cos \angle ADB}\cdot \dfrac{\cos \angle CDA}{DC}=\dfrac{AD}{AD}=1$ .
Άρα αν

η προβολή του

στην

θα είναι

μέσο του

οπότε το

ανήκει στην μεσοκάθετο του

και το λήμμα αποδείχθηκε.
Λήμμα 2 :

: 234.PNG (31.01 KiB) Προβλήθηκε 1081 φορές

Στο παραπάνω σχήμα θα ισχύει $\angle BNC=2\angle BKD$

Απόδειξη :

Είναι απλό να δούμε ότι αρκεί να ισχύει $\angle NBC=\angle NCB=\theta$ .
Έστω ότι οι DK,DL

τέμουν ξανά τον κύκλο στα P,Q

αντίστοιχα.Έστω ακόμη ότι $N'\equiv CP\cap BQ$ .
Από Pascal για τις (P,A,Q),(B,D,C)

έπεται ότι K,L,N'

συνευθειακά και μάλιστα $\angle N'BC=\angle QBC=\theta =\angle N'CB$ οπότε το

ανήκει στην μεσοκάθετο του

δηλαδή $N\equiv N'$ και το λημμα αποδείχθηκε.

Πάμε στην άσκηση:

: 235.PNG (27.91 KiB) Προβλήθηκε 1081 φορές

Εύκολα βλέπουμε πως $\angle NHB=\angle FHC$ και έτσι από το λήμμα 1 το MNF

θα είναι ισοσκελές.
Από το λήμμα 2 θα είναι $\angle FMN=2\cdot 18^{\circ}=36^{\circ}$ από όπου έπεται ότι $\angle MNF=\angle MFN=72^{\circ}$

Ορέστης Λιγνός · #3

Γιώργος Μήτσιος έγραψε: ↑
Πέμ Φεβ 20, 2020 12:48 pm
Καλό μεσημέρι σε όλους.

Στο εσωτερικό του τριγώνου υπάρχει σημείο ώστε να είναι $\widehat{ABH}=\widehat{ACH}=18^\circ$

ενώ είναι το μέσον της . Ο κύκλος με διάμετρο τέμνει τις στα και αντιστοίχως.

Να εξεταστεί η ιερότητα του τριγώνου (Να βρεθούν τα μέτρα των γωνιών του). Σας ευχαριστώ, Γιώργος.

Καλημέρα Γιώργο και Πρόδρομε.

Η λύση μου χωρίζεται σε 2 βήματα :

Βήμα 1 : Ισχύει, MN=MF

.

Έστω σημείο

ώστε το

να είναι παραλληλόγραμμο. Τότε, είναι προφανές ότι η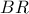

περνά από το μέσο της

που είναι το κέντρο

του κύκλου διαμέτρου

.

Οπότε, είναι $\angle ARH=\angle ABH=\angle ACH$ , άρα το ARCH

είναι εγγράψιμο.

Αν τώρα $X \equiv NF \cap RC$ , είναι $\angle NXC=\pi-\angle XFC-\angle FCX=\pi -\angle AFN-\angle ACR=\pi-\angle AFN-\angle AHR=$ $\pi -\angle AFN-\angle BAH=\pi -\angle AHN-\angle BAH=\pi/2$ , άρα $NF \perp RC$ .

Επίσης, έχουμε BO=OR, BM=MC

, συνεπώς $MO \parallel RC$ , και αφού $NF \perp BC \Rightarrow MO \perp NF$ , και αφού ON=OF

, θα προκύψει MN=MF

.

: vhma1.png (33.34 KiB) Προβλήθηκε 1045 φορές

Βήμα 2 : Ισχύει, $NMF=2\angle ABH=2\angle ACH$ .

Έστω, H',H'',H'''

τα συμμετρικά του

ως προς τα N,F,M

αντίστοιχα. Τότε, είναι H'N=NH, HM=MH''', HF=FH''

οπότε

και προφανώς τα $\vartriangle NFM, \vartriangle H'H''H'''$ είναι ομοιόθετα.

Τώρα, αφού MB=MC, HM=MH'''

, το

είναι παραλληλόγραμμο, οπότε CH'''=BH=BH'

και

.

Άρα τα τρίγωνα $\vartriangle BH'H'''$ και CH''H'''

είναι ίσα από Π-Π-Π, οπότε $\angle BH'H'''=\angle H''H'''C, \, \angle H'H'''B=\angle H'''H''C$ .

Άρα, $\angle H'H''H'''=\angle BH'''C-\angle H'H'''B-\angle H''H'''C=$ $\angle BHC-\angle H'H'''B-\angle BH'H'''=\angle BHC- (\pi -\angle H'BH''')=$ $\angle BHC+\angle H'BA+\angle B + \angle CBH'''-\pi=$ $\angle BHC+\angle ABH+ \angle B + \angle HCB-\pi=\angle ABH+\angle B-\angle HBC=2\angle ABH$ .

Αφού όμως τα $\vartriangle NFM, \vartriangle H'H''H'''$ είναι ομοιόθετα, έχω $\angle NMF=\angle H'H'''H''=2\angle ABH$ .

: vhma2.png (50.88 KiB) Προβλήθηκε 1045 φορές

Από τα Βήματα 1 και 2 τέλος, έχουμε ότι $\angle NMF=2\angle ABH = 36^\circ$ και $\angle FNM=\angle NFM=72^\circ$ .

min## · #4

Φέρτε την προβολή

του

στην

.Τα

είναι ομοκυκλικά οπότε έπονται τα πάντα.

#5

min## έγραψε: ↑
Παρ Φεβ 21, 2020 11:33 am
Φέρτε την προβολή του στην .Τα είναι ομοκυκλικά οπότε έπονται τα πάντα.

Πολύ σωστά!

Ορέστης Λιγνός · #6

min## έγραψε: ↑
Παρ Φεβ 21, 2020 11:33 am
Φέρτε την προβολή του στην .Τα είναι ομοκυκλικά οπότε έπονται τα πάντα.

Μίνο θα μπορούσες να γράψεις αναλυτικά τη λύση σου;

Ορέστης.

angvl · #7

: ιερό τρίγωνο.png (282.29 KiB) Προβλήθηκε 870 φορές

Καλησπέρα! Μετά τις εντυπωσιακές λύσεις που έδωσαν ο Πρόδρομος και ο Ορέστης, προσπάθησα με την υπόδειξη του min να δείξω ότι τα σημεία
N,F,M,K

είναι ομοκυκλικά αλλά δεν βγαίνει.....

Τα

και

εύκολα προκύπτουν ότι είναι ομοκυκλικά , επίσης εχώ βρεί αλλά δύο τρίγωνα με γωνίες 36^0,72^0,72^0

αλλά για το $\triangle NFM$ δεν βρήκα ακόμα κάτι. Τι δεν βλέπω ;

min## · #8

Η πρόταση κλειδί είναι ότι "Ισογώνια σημεία έχουν τον ίδιο ποδικό κύκλο".Το Ισογώνιο όμως του

ως προς το ABC

βρίσκεται στη μεσοκάθετο της

οπότε ο ποδικός κύκλος περιέχει το

.
Σημ.Προφανώς τα μέτρα των γωνιών που δίνονται δεν παίζουν ιδιαίτερο ρόλο..

#9

angvl έγραψε: ↑
Δευ Φεβ 24, 2020 10:37 pm
ιερό τρίγωνο.png

Καλησπέρα! Μετά τις εντυπωσιακές λύσεις που έδωσαν ο Πρόδρομος και ο Ορέστης, προσπάθησα με την υπόδειξη του min να δείξω ότι τα σημεία
είναι ομοκυκλικά αλλά δεν βγαίνει.....

Τα και εύκολα προκύπτουν ότι είναι ομοκυκλικά , επίσης εχώ βρεί αλλά δύο τρίγωνα με γωνίες
αλλά για το $\triangle NFM$ δεν βρήκα ακόμα κάτι. Τι δεν βλέπω ;

Ας δούμε στοιχειωδώς όσα αναφέρει ο Μίνος

Πάρε (στο σχήμα σου) και

το μέσο της

. Τότε (πολύ εύκολα από τα μέσα και το σχηματιζόμενο παραλληλόγραμμο.. ) βρίσκεις ότι $\vartriangle NEM=\vartriangle MZF\Rightarrow MN=MF$
Γωνιακά είναι ιδιαίτερα τώρα εύκολο να δείξεις ότι $\angle FMN=2\cdot \left( \angle HBN \right)=\angle NKF$ οπότε το επίμαχο τετράπλευρο που αναφέρει ο Μίνος είναι εγγράψιμο

#10

Άλλη μία απόδειξη για την εγγραψιμότητα του NFMK.

Φέρνω $\displaystyle HK \bot BC$ και γράφω τον περίκυκλο

του KNF

που επανατέμνει την

στο

και την

στο

Αρκεί να δείξω ότι BM=MC.

: Ιερότητα γωνίας.png (37.21 KiB) Προβλήθηκε 781 φορές

$\displaystyle \bullet$ Με τη βοήθεια των εγγράψιμων BNHK, CFHK

αποδεικνύουμε ότι η

είναι διχοτόμος της $N\widehat KF$ άρα και η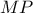

της $N\widehat MF$ και στη συνέχεια ότι MN=MF.

$\displaystyle \bullet$ Με κυνήγι γωνιών αποδεικνύουμε ότι τα τρίγωνα BNM, HNP

είναι όμοια, καθώς επίσης και τα HPF, MFC,

άρα:

$\displaystyle \frac{{BM}}{{PH}} = \frac{{MN}}{{PN}} = \frac{{MF}}{{PF}} = \frac{{MC}}{{PH}} \Rightarrow$ $\boxed{BM=MC}$

Γιώργος Μήτσιος · #11

Καλημέρα! Σας ευχαριστώ όλους για τη συμβολή σας κι' ένα επιπλέον εύγε στα νιάτα!
Με την ευκαιρία να δώσω κι΄εγώ τα συγχαρητήρια σε όλους τους διακριθέντες του διαγωνισμού Αρχιμήδης 2020 και ιδιαίτερα
στους Ορέστη Λιγνό , Πρόδρομο Φωτιάδη,Διονύση Αδαμόπουλο , Κων/νο Κωνσταντινίδη με ευχές για ανώτερες διακρίσεις!

Υποβάλλω στη συνέχεια και τη λύση που είχα στο νου , κατά τη δημοσίευση του παρόντος. (Σχετική βεβαίως η υπόδειξη πιο πριν του Στάθη)

: Ιερότητα τριγώνου ΙΙ.PNG (15.35 KiB) Προβλήθηκε 704 φορές

Η

είναι διάμετρος άρα $HN \perp AB$ και $HF \perp AC$ . ΟΙ

και

είναι διάμεσοι στα ορθ. τρίγωνα BHN

και

, έτσι τα

και

είναι του τύπου $36^\circ,72^\circ,72^\circ$ .Τα τρίγωνα IFM,LMN

είναι ίσα (κριτήριο ΠΓΠ) άρα $\boxed {MF=MN}$ .

Θα δείξουμε ότι το τρίγωνο FHN

είναι όμοιο με τα IFM,LMN

. Πράγματι έχουμε $\dfrac{HL}{HN}=\Phi =\dfrac{IF}{HF}\Rightarrow \dfrac{HN}{HF}=\dfrac{HL}{IF}=\dfrac{LN}{LM}$

ενώ $\widehat{FHN}=180^\circ -\widehat{A}$ , $\widehat{LHI}=36^\circ +\widehat{A}$ και $\widehat{MLN}=..=180^\circ -\widehat{A}$ οπότε $\widehat{FHN}=\widehat{MLN}$ .

Τότε $\widehat{MFN}=\widehat{MNF}=\theta +\widehat{HNM}=\widehat{HNL}=72^\circ$ .

Έθεσα , κατά τη σύνθεση του θέματος , γωνίες $18^ \circ$ ώστε το ισοσκελές MNF

να είναι του τύπου $36^\circ,72^\circ,72^\circ$
με λόγο σκέλους προς τη βάση τον γνωστό χρυσό αριθμό $\Phi$ . Ένα τέτοιο τρίγωνο εθεωρείτο (και) στην Αρχαία Ελλάδα από τα ιερά τρίγωνα.

Φιλικά, Γιώργος.

Ιερότητα τριγώνου

Ιερότητα τριγώνου

Re: Ιερότητα τριγώνου

Re: Ιερότητα τριγώνου

Re: Ιερότητα τριγώνου

Re: Ιερότητα τριγώνου

Re: Ιερότητα τριγώνου

Re: Ιερότητα τριγώνου

Re: Ιερότητα τριγώνου

Re: Ιερότητα τριγώνου

Re: Ιερότητα τριγώνου

Re: Ιερότητα τριγώνου

Μέλη σε σύνδεση