 είναι πολυώνυμο βαθμού
είναι πολυώνυμο βαθμού  και για αυτό ισχύει
και για αυτό ισχύει 
Να δειχθεί ότι το
 είναι παράγοντας του
είναι παράγοντας του  και αν
και αν 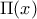 το πηλίκο , τότε να δειχθεί ότι η εξίσωση
το πηλίκο , τότε να δειχθεί ότι η εξίσωση  έχει ρίζες αντίστροφους αριθμούς ανά δύο.
έχει ρίζες αντίστροφους αριθμούς ανά δύο.Συντονιστής: exdx

 τότε
τότε  προσθέτοντας και θέτοντας πολυώνυμο
προσθέτοντας και θέτοντας πολυώνυμο  έχουμε
έχουμε Για να ισχύει για κάθε
Για να ισχύει για κάθε  πρέπει
πρέπει και τα λοιπά εκτός από τον μεσαίο συντελεστή που θα είναι
και τα λοιπά εκτός από τον μεσαίο συντελεστή που θα είναι  αφού το
αφού το  είναι το μηδενικό πολυώνυμο. Οπότε τώρα θα έχουμε
είναι το μηδενικό πολυώνυμο. Οπότε τώρα θα έχουμε
 έτσι μπορούμε να παραγοντοποιήσουμε όλο το πολυώνυμο και να βγάλουμε κοινό παράγοντα το
έτσι μπορούμε να παραγοντοποιήσουμε όλο το πολυώνυμο και να βγάλουμε κοινό παράγοντα το  Οπότε το
Οπότε το  διαιρεί το
διαιρεί το  τέλεια, το δεύτερο θα το δω πιο μετά
τέλεια, το δεύτερο θα το δω πιο μετάΠιο απλά: ΘέτονταςTolaso J Kos έγραψε: ↑Παρ Δεκ 21, 2018 10:44 amΤοείναι πολυώνυμο βαθμού
και για αυτό ισχύει

Να δειχθεί ότι τοείναι παράγοντας του
και αν
το πηλίκο , τότε να δειχθεί ότι η εξίσωση
έχει ρίζες αντίστροφους αριθμούς ανά δύο.
 στην δοθείσα, είναι
στην δοθείσα, είναι  . Άρα
. Άρα  , που σημαίνει ότι η
, που σημαίνει ότι η  είναι ρίζα. Όμοια η
είναι ρίζα. Όμοια η 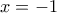 δίνει
δίνει  . Άρα
. Άρα  , που σημαίνει ότι η
, που σημαίνει ότι η 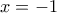 είναι ρίζα. Άρα το
είναι ρίζα. Άρα το  έχει παράγοντα το
έχει παράγοντα το  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες