 είναι η διχοτόμος τριγώνου
είναι η διχοτόμος τριγώνου  και επί των πλευρών του
και επί των πλευρών του  θεωρώ τα σημεία
θεωρώ τα σημεία  αντίστοιχα, ώστε
αντίστοιχα, ώστε  Αν
Αν  είναι το
είναι το 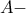 παράκεντρο του τριγώνου
παράκεντρο του τριγώνου  να δείξετε ότι το
να δείξετε ότι το  είναι εγγράψιμο.
είναι εγγράψιμο.Συντονιστής: Μιχάλης Νάννος
 είναι η διχοτόμος τριγώνου
είναι η διχοτόμος τριγώνου  και επί των πλευρών του
και επί των πλευρών του  θεωρώ τα σημεία
θεωρώ τα σημεία  αντίστοιχα, ώστε
αντίστοιχα, ώστε  Αν
Αν  είναι το
είναι το 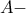 παράκεντρο του τριγώνου
παράκεντρο του τριγώνου  να δείξετε ότι το
να δείξετε ότι το  είναι εγγράψιμο.
είναι εγγράψιμο.george visvikis έγραψε:είναι η διχοτόμος τριγώνου
και επί των πλευρών του
θεωρώ τα σημεία
αντίστοιχα, ώστε
Αν
είναι το
παράκεντρο του τριγώνου
να δείξετε ότι το
είναι εγγράψιμο.
 στην πλευρά
στην πλευρά  ώστε
ώστε  .
. , άρα
, άρα  .
. , έχουμε
, έχουμε  .
.
 , οπότε
, οπότε  (1).
(1). είναι το
είναι το  - παράκεντρο του
- παράκεντρο του  , οπότε εύκολα με γωνίες
, οπότε εύκολα με γωνίες  (2).
(2). , άρα το
, άρα το  είναι εγγράψιμο, οπότε
είναι εγγράψιμο, οπότε  .
. , οπότε
, οπότε  , συνεπώς
, συνεπώς  .
. σημείο της
σημείο της  με
με  . Κάθε μια από τις γωνίες
. Κάθε μια από τις γωνίες  είναι ίση με
είναι ίση με  άρα το τετράπλευρο
άρα το τετράπλευρο  είναι εγγράψιμο και έτσι
είναι εγγράψιμο και έτσι  που μας
που μας Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες