Στο παρακάτω σχήμα τα τρίγωνα
 και
και  έχουν ίσες περιμέτρους. Να αποδείξετε ότι:
έχουν ίσες περιμέτρους. Να αποδείξετε ότι: 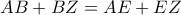
Συντονιστής: Μιχάλης Νάννος
 και
και  έχουν ίσες περιμέτρους. Να αποδείξετε ότι:
έχουν ίσες περιμέτρους. Να αποδείξετε ότι: 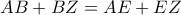
Καλημέρα.ghan έγραψε:Μία ενδιαφέρουσα άσκηση που βρήκα στο Facebook δημοσιευμένη στις 22 / 11 / 2015 από τον Αντώνη Κυριακόπουλο.
Στο παρακάτω σχήμα τα τρίγωνακαι
έχουν ίσες περιμέτρους. Να αποδείξετε ότι:
 ο
ο  παρεγγεγραμμένος κύκλος του τριγώνου
παρεγγεγραμμένος κύκλος του τριγώνου  που εφάπτεται στις
που εφάπτεται στις  στα σημεία
στα σημεία  αντίστοιχα, και
αντίστοιχα, και  η κοινή ημιπερίμετρος των δύο τριγώνων. Είναι
η κοινή ημιπερίμετρος των δύο τριγώνων. Είναι  , οπότε ο
, οπότε ο  είναι ο
είναι ο  παρεγγεγραμμένος κύκλος και του τριγώνου
παρεγγεγραμμένος κύκλος και του τριγώνου  και έστω
και έστω  το σημείο επαφής του με την
το σημείο επαφής του με την  .
.
 , θα είναι:
, θα είναι: 
Ευχαριστώ τον κύριο Γιώργο Βισβίκη για την ευφυέστατη λύση του.george visvikis έγραψε:Καλημέρα.ghan έγραψε:Μία ενδιαφέρουσα άσκηση που βρήκα στο Facebook δημοσιευμένη στις 22 / 11 / 2015 από τον Αντώνη Κυριακόπουλο.
Στο παρακάτω σχήμα τα τρίγωνακαι
έχουν ίσες περιμέτρους. Να αποδείξετε ότι:
Έστωο
παρεγγεγραμμένος κύκλος του τριγώνου
που εφάπτεται στις
στα σημεία
αντίστοιχα, και
η κοινή ημιπερίμετρος των δύο τριγώνων. Είναι
, οπότε ο
είναι ο
παρεγγεγραμμένος κύκλος και του τριγώνου
και έστω
το σημείο επαφής του με την
.
και επειδή, θα είναι:
Γιώργο, κάπου το είχα δει λυμένο αυτό το πρόβλημα σε ένα αγγλικό βιβλίο διαγωνισμών , αλλά δεν θυμάμαι να είχε τόσο καλή λύση.george visvikis έγραψε:Καλημέρα.ghan έγραψε:Μία ενδιαφέρουσα άσκηση που βρήκα στο Facebook δημοσιευμένη στις 22 / 11 / 2015 από τον Αντώνη Κυριακόπουλο.
Στο παρακάτω σχήμα τα τρίγωνακαι
έχουν ίσες περιμέτρους. Να αποδείξετε ότι:
Έστωο
παρεγγεγραμμένος κύκλος του τριγώνου
που εφάπτεται στις
στα σημεία
αντίστοιχα, και
η κοινή ημιπερίμετρος των δύο τριγώνων. Είναι
, οπότε ο
είναι ο
παρεγγεγραμμένος κύκλος και του τριγώνου
και έστω
το σημείο επαφής του με την
.
και επειδή, θα είναι:
 Το πρόβλημα αυτό έρχεται από το παρελθόν. Στο βιβλίο Γεωμετρίας Ιησουϊτών (*), σελίδα 333, υπάρχει ως θεώρημα 157, η ακόλουθη πρόταση με αναφορά στον Steiner και χρονολογία 1846.
Το πρόβλημα αυτό έρχεται από το παρελθόν. Στο βιβλίο Γεωμετρίας Ιησουϊτών (*), σελίδα 333, υπάρχει ως θεώρημα 157, η ακόλουθη πρόταση με αναφορά στον Steiner και χρονολογία 1846. Πράγματι, στο σχήμα του Γιώργου πιο πάνω, έστω ότι ο
Πράγματι, στο σχήμα του Γιώργου πιο πάνω, έστω ότι ο  -παρεγγεγραμμένος κύκλος του τριγώνου
-παρεγγεγραμμένος κύκλος του τριγώνου  εφάπτεται της πλευράς
εφάπτεται της πλευράς  στο σημείο
στο σημείο  και έστω ότι η δια του σημείου
και έστω ότι η δια του σημείου  εφαπτομένη του ιδίου κύκλου, τέμνει τις
εφαπτομένη του ιδίου κύκλου, τέμνει τις  , στα σημεία
, στα σημεία  , αντιστοίχως και ας είναι το
, αντιστοίχως και ας είναι το  μεταξύ των
μεταξύ των  οπότε το
οπότε το  θα είναι μεταξύ των
θα είναι μεταξύ των  .
. έχουμε
έχουμε 
 και
και 
 που θεωρείται ότι ισχύει στο τετράπλευρο
που θεωρείται ότι ισχύει στο τετράπλευρο 
 , προκύπτει ότι
, προκύπτει ότι 
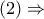
 και άρα, η
και άρα, η  εφάπτεται στον
εφάπτεται στον  -παρεγγεγραμμένο κύκλο του
-παρεγγεγραμμένο κύκλο του  και το τετράπλευρο
και το τετράπλευρο  είναι παρεγγράψιμο.
είναι παρεγγράψιμο.
 στο σχήμα του Γιώργου
στο σχήμα του Γιώργου  προκύπτει ως άμεσο αποτέλεσμα ότι τα τρίγωνα
προκύπτει ως άμεσο αποτέλεσμα ότι τα τρίγωνα  είναι ισοπεριμετρικά.
είναι ισοπεριμετρικά.
 .
.Ευχαριστώ πολύ τον κύριο Βήτα που μου θύμισε το τέταρτο θέμα Γεωμετρίας (εδώ) που είχε τεθεί τοvittasko έγραψε:Το πρόβλημα αυτό έρχεται από το παρελθόν. Στο βιβλίο Γεωμετρίας Ιησουϊτών (*), σελίδα 333, υπάρχει ως θεώρημα 157, η ακόλουθη πρόταση με αναφορά στον Steiner και χρονολογία 1846.
Σε κάθε παρεγγράψιμο τετράπλευρο, η διαφορά δύο απέναντι πλευρών του είναι ίση με την διαφορά των δύο άλλων.
Σε συνδυασμό με το θεώρημα 158 τώρα, στην σελίδα 334, ισχύει και το αντίστροφο.
Εάν σε ένα τετράπλευρο η διαφορά δύο πλευρών του είναι ίση με την διαφορά των δύο άλλων, τότε το τετράπλευρο είναι παρεγγράψιμο.
Έχουμε δηλαδή τις ίσες διαφορές των απέναντι πλευρών ως κριτήριο παρεγγραψιμότητας ενός τετραπλεύρου, όπως έχουμε τα ίσα αθροίσματα των απέναντι πλευρών, ως κριτήριο περιγραψιμότητας .
Η απόδειξη του αντίστροφου για το παρεγγράψιμο τετράπλευρο είναι εύκολη.
 στη ΣΜΑ και βασιζόταν σ’ αυτήν ακριβώς την ιδιότητα των παρεγγράψιμων τετραπλεύρων και μάλιστα κυρτών ή μη κυρτών.
στη ΣΜΑ και βασιζόταν σ’ αυτήν ακριβώς την ιδιότητα των παρεγγράψιμων τετραπλεύρων και μάλιστα κυρτών ή μη κυρτών.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης