Να βρείτε το διάστημα σύγκλισης έστω
 της δυναμοσειράς
της δυναμοσειράς 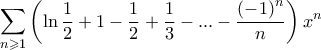 , καθώς και το άθροισμα για κάθε τιμή του
, καθώς και το άθροισμα για κάθε τιμή του 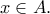
Υ.Γ Θα αφήσω όσο χρόνο επιθυμείτε μέχρι να ανεβάσω τη λύση μου.
Συντονιστής: Demetres
 της δυναμοσειράς
της δυναμοσειράς 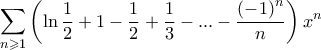 , καθώς και το άθροισμα για κάθε τιμή του
, καθώς και το άθροισμα για κάθε τιμή του 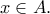
 είναι εκφυλισμένο διάστημα με ακτίνα
είναι εκφυλισμένο διάστημα με ακτίνα  , υπάρχει πάντα ακτίνα σύγκλισης.
, υπάρχει πάντα ακτίνα σύγκλισης.![limsup\sqrt[n]{\left | a_{n} \right |}=l limsup\sqrt[n]{\left | a_{n} \right |}=l](/forum/ext/geomar/texintegr/latexrender/pictures/18a8e1b9cbfe5a841d61583c402ecaf3.png) .
. , όπως προκύπτει αν θέσουμε
, όπως προκύπτει αν θέσουμε  , στη σειρά Maclaurin της
, στη σειρά Maclaurin της 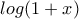 .
.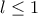 .
.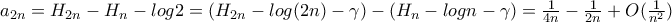 .
.![4n\left | a_{2n} \right |\rightarrow 1\Rightarrow \sqrt[2n]{4n\left | a_{2n} \right |}\rightarrow 1 4n\left | a_{2n} \right |\rightarrow 1\Rightarrow \sqrt[2n]{4n\left | a_{2n} \right |}\rightarrow 1](/forum/ext/geomar/texintegr/latexrender/pictures/faaf4eb372a32f88cb53e3c3e8ae65f9.png)
![\sqrt[2n]{4n}\rightarrow 1 \sqrt[2n]{4n}\rightarrow 1](/forum/ext/geomar/texintegr/latexrender/pictures/63e461105fb132e1f7ad2f49bfa69d93.png) , έπεται ότι
, έπεται ότι ![\sqrt[2n]{\left | a_{2n} \right |}\rightarrow 1 \sqrt[2n]{\left | a_{2n} \right |}\rightarrow 1](/forum/ext/geomar/texintegr/latexrender/pictures/62e0e2a65a472cff5a8688a6cb68c2aa.png) και επειδή
και επειδή 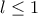 ,
, .
.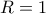 .
.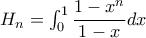 .
.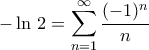
 γράφεται
γράφεται 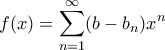 όπου
όπου 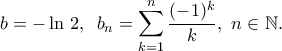
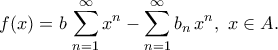
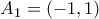 και όριο
και όριο 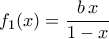
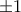 δεν έχουμε σύγκλιση διότι
δεν έχουμε σύγκλιση διότι 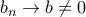 . Τελικά η
. Τελικά η  συγκλίνει στο
συγκλίνει στο 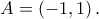
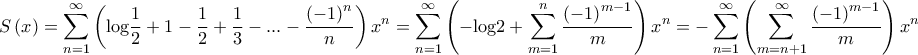
![\displaystyle \lim_{n\rightarrow +\infty}\sqrt[n]{ \left | \sum_{m=n+1}^{\infty}\frac{\left ( -1 \right )^{m-1}}{m} \right |\cdot \left | x \right |^{n}}=\left | x \right |, \displaystyle \lim_{n\rightarrow +\infty}\sqrt[n]{ \left | \sum_{m=n+1}^{\infty}\frac{\left ( -1 \right )^{m-1}}{m} \right |\cdot \left | x \right |^{n}}=\left | x \right |,](/forum/ext/geomar/texintegr/latexrender/pictures/c906e557318c6967ac7ea18d2d7d648e.png) η δυναμοσειρά συγκλίνει για
η δυναμοσειρά συγκλίνει για  και αποκλίνει για
και αποκλίνει για 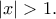
 Είναι
Είναι 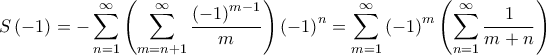 που αποκλίνει.
που αποκλίνει. Για
Για 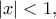 είναι
είναι 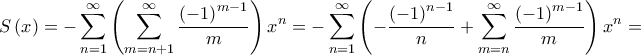

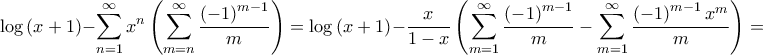
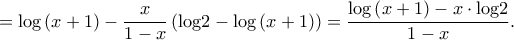
 Για
Για  είναι
είναι 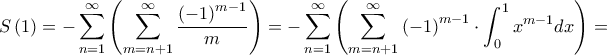
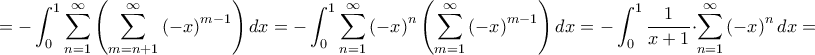
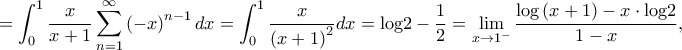
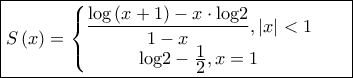 και αποκλίνει για
και αποκλίνει για 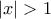 και για
και για 
Έμεινε να βρεθεί το άθροισμα.
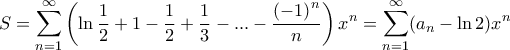
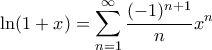 έχουμε
έχουμε 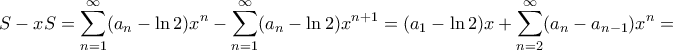
![\displaystyle{= (a_1-\ln 2)x + \sum_{n= 2}^{\infty } \dfrac {(-1)^{n+1}}{n} x^n= (a_1-\ln 2)x + [ \ln (1+x)-x]= \ln(1+x)- x\ln 2 } \displaystyle{= (a_1-\ln 2)x + \sum_{n= 2}^{\infty } \dfrac {(-1)^{n+1}}{n} x^n= (a_1-\ln 2)x + [ \ln (1+x)-x]= \ln(1+x)- x\ln 2 }](/forum/ext/geomar/texintegr/latexrender/pictures/16428dd4921e82ae09cb0c8f1a2a5aa9.png)
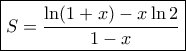 για
για  . Για
. Για  άμεσο από τα παραπάνω.
άμεσο από τα παραπάνω. .
![\displaystyle \lim_{n\rightarrow +\infty}\sqrt[n]{ \left | a_n \right |} \displaystyle \lim_{n\rightarrow +\infty}\sqrt[n]{ \left | a_n \right |}](/forum/ext/geomar/texintegr/latexrender/pictures/2f09aac1c25a066238f793238848c52d.png) (που ισούται με
(που ισούται με  ) είναι αυτό που μας δίνει την ακτίνα σύγκλισης (το
) είναι αυτό που μας δίνει την ακτίνα σύγκλισης (το 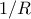 ισούται με αυτό).
ισούται με αυτό).Προφανώς, απλά δεν αναφέρθηκα στην ακτίνα σύγκλισης, αυτό θέλω να πω.Mihalis_Lambrou έγραψε: ↑Παρ Δεκ 29, 2023 8:48 pm.
Σωστά αλλά ουσιαστικά χρησιμοποιεί ακτίνα σύγκλισης στα κρυφά: Το παραπάνω όριο των συντελεστών, εδώ της μορφής(που ισούται με
) είναι αυτό που μας δίνει την ακτίνα σύγκλισης (το
ισούται με αυτό).
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης