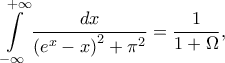 όπου
όπου  είναι η μοναδική πραγματική ρίζα της εξίσωσης
είναι η μοναδική πραγματική ρίζα της εξίσωσης 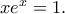
Συντονιστής: Demetres
Μη αναγνωσμένη δημοσίευση από Dimessi » Τρί Ιαν 02, 2024 4:36 pm
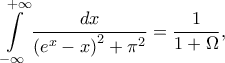 όπου
όπου  είναι η μοναδική πραγματική ρίζα της εξίσωσης
είναι η μοναδική πραγματική ρίζα της εξίσωσης 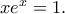
Μη αναγνωσμένη δημοσίευση από Dimessi » Πέμ Ιαν 11, 2024 4:24 pm
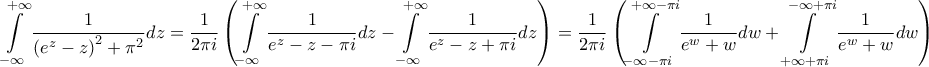 και
και 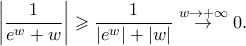 Έστω
Έστω  το ορθογώνιο με κορυφές
το ορθογώνιο με κορυφές 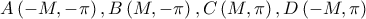 με
με  και με ορθή φορά περιστροφής. Η συνάρτηση
και με ορθή φορά περιστροφής. Η συνάρτηση 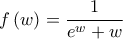 είναι μερόμορφη στο εσωτερικό του ορθογωνίου
είναι μερόμορφη στο εσωτερικό του ορθογωνίου  (είναι αναλυτική με κάποιους πόλους) και θα βρούμε τους πόλους της
(είναι αναλυτική με κάποιους πόλους) και θα βρούμε τους πόλους της 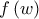 στο εσωτερικό του ορθογωνίου
στο εσωτερικό του ορθογωνίου 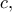 επομένως τις ρίζες τις εξίσωσης
επομένως τις ρίζες τις εξίσωσης 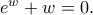 Έχουμε
Έχουμε  Για
Για  παίρνουμε
παίρνουμε 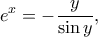 που είναι αδύνατη για
που είναι αδύνατη για ![y\in \left [ -\pi ,\pi \right ]. y\in \left [ -\pi ,\pi \right ].](/forum/ext/geomar/texintegr/latexrender/pictures/8714e774a53c60ceb50a8ac6bb7fd9bb.png) Για
Για 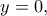 ρίζα είναι η μοναδική πραγματική ρίζα της εξίσωσης
ρίζα είναι η μοναδική πραγματική ρίζα της εξίσωσης 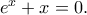 Επομένως, αν
Επομένως, αν  η ρίζα της εξίσωσης
η ρίζα της εξίσωσης 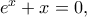 παίρνουμε
παίρνουμε 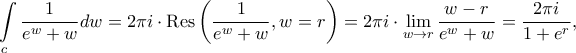 άρα
άρα 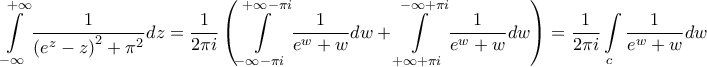
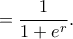 Αφού
Αφού 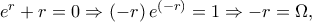 όπου
όπου  είναι η μοναδική πραγματική ρίζα της εξίσωσης
είναι η μοναδική πραγματική ρίζα της εξίσωσης 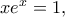 συνεπώς
συνεπώς 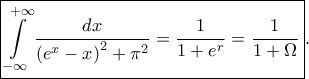
Επιστροφή σε “Ανάλυση (Φοιτητές)”
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης
Powered by phpBB® Forum Software © phpBB Limited
Style από Arty - Ενημέρωση phpBB 3.2 από MrGaby
Ελληνική μετάφραση από το phpbbgr.com
Το www.mathematica.gr δημιουργήθηκε από τους Γρηγόρη Κωστάκο και Αλέξανδρο Συγκελάκη
με τη βοήθεια των Στέλιου Μόσχογλου και Γιώργου Μαργαρίτη
GZIP: Off