 Η ακολουθία :
Η ακολουθία : 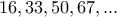 είναι ασφαλώς μια αριθμητική πρόοδος .
είναι ασφαλώς μια αριθμητική πρόοδος . Παρατηρήστε , ότι ο
 είναι τέλειο τετράγωνο . Μπορείτε να βρείτε τους τρεις
είναι τέλειο τετράγωνο . Μπορείτε να βρείτε τους τρειςεπόμενους όρους της προόδου , οι οποίοι είναι επίσης τέλεια τετράγωνα ;
Συντονιστής: stranton
 Η ακολουθία :
Η ακολουθία : 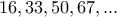 είναι ασφαλώς μια αριθμητική πρόοδος .
είναι ασφαλώς μια αριθμητική πρόοδος .  είναι τέλειο τετράγωνο . Μπορείτε να βρείτε τους τρεις
είναι τέλειο τετράγωνο . Μπορείτε να βρείτε τους τρεις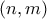 της εξίσωσης
της εξίσωσης 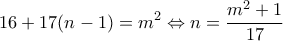 . Αυτό σημαίνει ότι πρέπει
. Αυτό σημαίνει ότι πρέπει 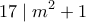 άρα το
άρα το 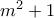 είναι πολλαπλάσιο του
είναι πολλαπλάσιο του  . Με δοκιμές βρίσκουμε ότι ότι οι ζητούμενοι όροι της ακολουθίας είναι ο
. Με δοκιμές βρίσκουμε ότι ότι οι ζητούμενοι όροι της ακολουθίας είναι ο  ος, ο
ος, ο 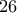 ος και ο
ος και ο  ος. Αντίστοιχα,
ος. Αντίστοιχα, 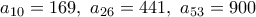 .
.Μπορούμε και χωρίς δοκιμές, όπως άλλωστε ρητά ζητάει η άσκηση.
Κ. Μιχάλη αλλιώς το κατάλαβα το "χωρίς δοκιμές" συγγνώμη. Αλλά που υπάρχει περιορισμός 24ώρου.Mihalis_Lambrou έγραψε: ↑Παρ Μαρ 18, 2022 1:21 pmΜπορούμε και χωρίς δοκιμές, όπως άλλωστε ρητά ζητάει η άσκηση.
Επειδή η άσκηση είναι ακόμα ανοικτή σε μαθητές, θα περιμένω να περάσουν οι 24 ώρες που έχει θέσει ο θεματοθέτης.
Εκεί θα σου δώσω δίκιο. Ο θεματοθέτης Θανάσης έχει τον δικό του κώδικα επικοινωνίας σύμφωνα με τον οποίο όταν βάζει ένα αστέρι
 στην αρχή της εκφώνησης, εννοεί περιορισμό
στην αρχή της εκφώνησης, εννοεί περιορισμό  ωρών για να ασχοληθούν οι μαθητές. Εννοείται ότι προκύπτει το ερώτημα από πού οφείλει να το ξέρει ο καθένας; Για παράδειγμα πώς θα το καταλάβει ένα νέο μέλος στο φόρουμ. Από την άλλη, η θεματοδότηση από τον Θανάση είναι τόσο πλούσια που τέτοια πρακτική, την οποία άλλωστε υιοθετεί καιρό τώρα, είναι απόλυτα κατανοητή και συγχωρείται αβίαστα.
ωρών για να ασχοληθούν οι μαθητές. Εννοείται ότι προκύπτει το ερώτημα από πού οφείλει να το ξέρει ο καθένας; Για παράδειγμα πώς θα το καταλάβει ένα νέο μέλος στο φόρουμ. Από την άλλη, η θεματοδότηση από τον Θανάση είναι τόσο πλούσια που τέτοια πρακτική, την οποία άλλωστε υιοθετεί καιρό τώρα, είναι απόλυτα κατανοητή και συγχωρείται αβίαστα.Για κάθε
 μη μηδενικό φυσικό ο γενικός όρος της προόδου γράφεται :
μη μηδενικό φυσικό ο γενικός όρος της προόδου γράφεται :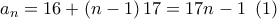 .
.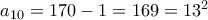 . Δηλαδή
. Δηλαδή 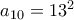

 με
με 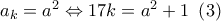 ,
,  φυσικός.
φυσικός.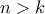 με
με 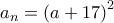 . Δηλαδή
. Δηλαδή 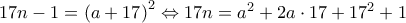 ή λόγω της
ή λόγω της 
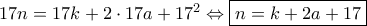
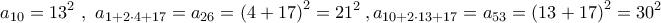
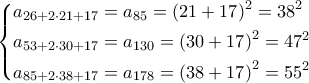 κ. λ. π.
κ. λ. π.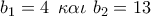 και μετά , για κάθε
και μετά , για κάθε  έχω:
έχω: 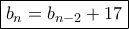 .
.To ζητούμενο γράφεται
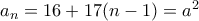 για κάποιον φυσικό
για κάποιον φυσικό  . Άρα
. Άρα 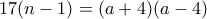 που σημαίνει ότι o πρώτος
που σημαίνει ότι o πρώτος  διαιρεί είτε τον
διαιρεί είτε τον 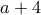 ή τον
ή τον  .
. ή
ή 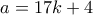 . Άρα
. Άρα 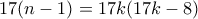 ή
ή 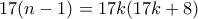 , ισοδύναμα
, ισοδύναμα 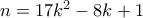 ή
ή 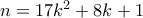 .
. 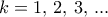 βρίσκουμε διαδοχικά τα αντίστοιχα
βρίσκουμε διαδοχικά τα αντίστοιχα  και από εκεί τα
και από εκεί τα  ως εξής:
ως εξής: 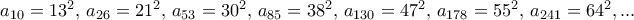
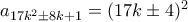
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες