 με
με 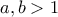 , τέτοια ώστε το
, τέτοια ώστε το  να διαιρεί το
να διαιρεί το 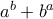 .
.Συντονιστές: cretanman, silouan, rek2
 με
με 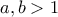 , τέτοια ώστε το
, τέτοια ώστε το  να διαιρεί το
να διαιρεί το 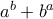 .
.Κάτι άλλο θα εννοείς γιατί ανJ. Robert Oppenheimer έγραψε: ↑Κυρ Οκτ 15, 2023 3:05 pmΝα δείξετε ότι υπάρχουν άπειρα το πλήθος ζεύγη σχετικά πρώτων θετικών ακεραίων αριθμών, τέτοια ώστε το
να διαιρεί το
.
 οποιοσδήποτε και αν
οποιοσδήποτε και αν  , τότε
, τότε 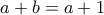 που διαιρεί τον
που διαιρεί τον 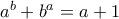 .
. Πράγματι, ξέχασα την συνθήκηMihalis_Lambrou έγραψε: ↑Κυρ Οκτ 15, 2023 4:20 pmΚάτι άλλο θα εννοείς γιατί ανJ. Robert Oppenheimer έγραψε: ↑Κυρ Οκτ 15, 2023 3:05 pmΝα δείξετε ότι υπάρχουν άπειρα το πλήθος ζεύγη σχετικά πρώτων θετικών ακεραίων αριθμών, τέτοια ώστε το
να διαιρεί το
.
οποιοσδήποτε και αν
, τότε
που διαιρεί τον
.
(Toυλάχιστον αυτό βλέπω στο αεροδρόμιο Θεσσαλονίκης που βρίσκομαι, μετά το πρώτο σκέλος κουραστικού ταξιδιού.)
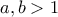 . Ευχαριστώ για την επισήμανση!
. Ευχαριστώ για την επισήμανση! πρώτος της μορφής
πρώτος της μορφής 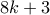 . Υπάρχουν άπειροι τέτοιο πρώτοι.
. Υπάρχουν άπειροι τέτοιο πρώτοι. 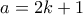 και
και 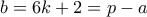 . Αρκεί να δείξουμε ότι
. Αρκεί να δείξουμε ότι 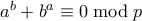 . Έχουμε
. Έχουμε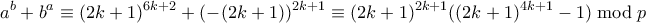
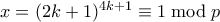 . Είναι
. Είναι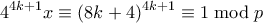
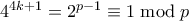 .
.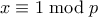 και
και 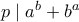 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες