Ποιο είναι το ελάχιστο δυνατό πλήθος στοιχείων που μπορούμε να σβήσουμε από το σύνολο
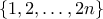 , ώστε το άθροισμα οποιωνδήποτε δύο να είναι σύνθετος αριθμός;
, ώστε το άθροισμα οποιωνδήποτε δύο να είναι σύνθετος αριθμός;Συντονιστές: cretanman, silouan, rek2
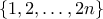 , ώστε το άθροισμα οποιωνδήποτε δύο να είναι σύνθετος αριθμός;
, ώστε το άθροισμα οποιωνδήποτε δύο να είναι σύνθετος αριθμός;Κύριε Λάμπρου,Ενδιαφέρον.
Έχω λύση με Θεώρημα Bertrand (βλέπε εδώ). Αυτό έχεις κατά νου, ή έχεις στοιχειώδη λύση;
Το ρωτάω, λόγω φακέλου.
 , το μέγιστο σύνολο με την εν λόγω ιδιότητα περιέχει τα μισά στοιχεία.
, το μέγιστο σύνολο με την εν λόγω ιδιότητα περιέχει τα μισά στοιχεία. .
. μεταξύ
μεταξύ  και
και  .
.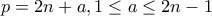 .
.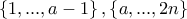 .
.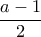 στοιχεία.
στοιχεία.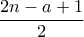 στοιχεία (π.χ. τους άρτιους).
στοιχεία (π.χ. τους άρτιους).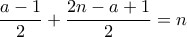 στοιχεία, π.χ. όλους τους άρτιους ή όλους τους περιττούς.
στοιχεία, π.χ. όλους τους άρτιους ή όλους τους περιττούς.Θα δείξουμε (ισχυροποιώντας το ζητούμενο) ότι τα μόνα μέγιστα υποσύνολα του
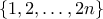 που μπορούν να παραμείνουν είναι α) οι άρτιοι και β) περιττοί του. Και στις δύο περιπτώσεις, μένει το μισό σύνολο.
που μπορούν να παραμείνουν είναι α) οι άρτιοι και β) περιττοί του. Και στις δύο περιπτώσεις, μένει το μισό σύνολο.  , απλό. Για το επαγωγικό βήμα, εξετάζουμε το
, απλό. Για το επαγωγικό βήμα, εξετάζουμε το 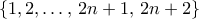 . Επειδή οι άρτιοι (ή οι περιττοί) είναι παράδειγμα συνόλου με τις ζητούμενες ιδιότητες, σημαίνει ότι το μέγιστο πλήθος στοιχείων του ζητούμενου υποσυνόλου είναι
. Επειδή οι άρτιοι (ή οι περιττοί) είναι παράδειγμα συνόλου με τις ζητούμενες ιδιότητες, σημαίνει ότι το μέγιστο πλήθος στοιχείων του ζητούμενου υποσυνόλου είναι 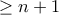 στοιχεία. Θα δείξουμε ότι έχει ακριβώς
στοιχεία. Θα δείξουμε ότι έχει ακριβώς  στοιχεία δείχνοντας ότι δεν μπορεί να είναι
στοιχεία δείχνοντας ότι δεν μπορεί να είναι 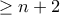 .
. 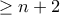 στοιχεία.
στοιχεία. 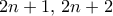 . Αν περιείχε και τα δύο τότε σβήνοντάς τα έπεται το μέγιστο υποσύνολο με τις ζητούμενες ιδιότητες του
. Αν περιείχε και τα δύο τότε σβήνοντάς τα έπεται το μέγιστο υποσύνολο με τις ζητούμενες ιδιότητες του 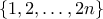 θα περιείχε
θα περιείχε 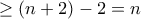 στοιχεία. Από την επαγωγική υπόθεση, το υποσύνολο του
στοιχεία. Από την επαγωγική υπόθεση, το υποσύνολο του 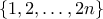 που προκύπτει έχει ακριβώς
που προκύπτει έχει ακριβώς  στοιχεία και είναι είτε οι περιττοί του ή οι άρτιοί του. Ας υποθέσουμε το πρώτο, από όπου θα δείξουμε ότι ο
στοιχεία και είναι είτε οι περιττοί του ή οι άρτιοί του. Ας υποθέσουμε το πρώτο, από όπου θα δείξουμε ότι ο 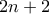 δεν βρίσκεται στο σύνολό μας, αντίθετα από την υπόθεση.
δεν βρίσκεται στο σύνολό μας, αντίθετα από την υπόθεση. 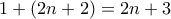 και
και 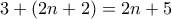 και ...
και ... 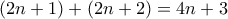 . Όμως από Θεώρημα Bertrand μεταξύ του
. Όμως από Θεώρημα Bertrand μεταξύ του  και του
και του  υπάρχει (περιττός) πρώτος (οι άρτιοι σίγουρα δεν είναι αυτός ο πρώτος). Αλλά αυτό συγκρούεται με την κατασκευή του υποσυνόλου.
υπάρχει (περιττός) πρώτος (οι άρτιοι σίγουρα δεν είναι αυτός ο πρώτος). Αλλά αυτό συγκρούεται με την κατασκευή του υποσυνόλου. 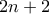 δεν βρίσκεται στο υποσύνολο. Άρα το ίδιο αποτελείται μόνο από περιττούς, όπως θέλαμε.
δεν βρίσκεται στο υποσύνολο. Άρα το ίδιο αποτελείται μόνο από περιττούς, όπως θέλαμε. 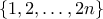 ήταν οι άρτιοι. Τελειώσαμε.
ήταν οι άρτιοι. Τελειώσαμε.Δεν «μπορούμε» να έχουμε λύση χωρίς Bertrand. Αν πάρουμε το υποσύνολοMihalis_Lambrou έγραψε: ↑Δευ Σεπ 11, 2023 7:44 pmΕνδιαφέρον.
Έχω λύση με Θεώρημα Bertrand (βλέπε εδώ). Αυτό έχεις κατά νου, ή έχεις στοιχειώδη λύση;
Το ρωτάω, λόγω φακέλου.
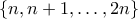 με
με  στοιχεία, για να δείξουμε ότι δεν μας κάνει, πρέπει να δείξουμε ότι τουλάχιστον ένας από τους
στοιχεία, για να δείξουμε ότι δεν μας κάνει, πρέπει να δείξουμε ότι τουλάχιστον ένας από τους 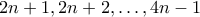 είναι πρώτος. Που είναι ουσιαστικά το Bertrand.
είναι πρώτος. Που είναι ουσιαστικά το Bertrand.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες