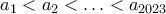 τέτοιοι, ώστε
τέτοιοι, ώστε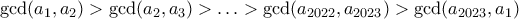 .
.Συντονιστές: cretanman, silouan, rek2
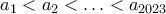 τέτοιοι, ώστε
τέτοιοι, ώστε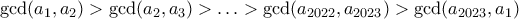 .
.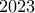 πρώτους μεγαλύτρους του
πρώτους μεγαλύτρους του  με
με 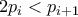 και
και 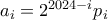 , για κάθε
, για κάθε 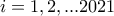 ,
,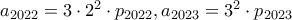
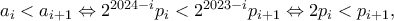 και με τον ίδιο τρόπο
και με τον ίδιο τρόπο 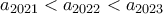 το οποίο ισχύει λόγω της αρχικής επιλογής που κάναμε.
το οποίο ισχύει λόγω της αρχικής επιλογής που κάναμε.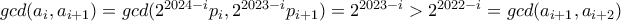 και
και 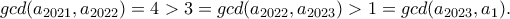
Για τυπογραφική ευκολία θα το κάνω γιαΟρέστης Λιγνός έγραψε: ↑Δευ Μαρ 27, 2023 10:00 pmΝα αποδείξετε ότι υπάρχουν θετικοί ακέραιοιτέτοιοι, ώστε
.
 αριθμούς αντί
αριθμούς αντί 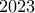 , αλλά γενικεύεται απλά.
, αλλά γενικεύεται απλά. 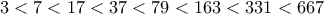 .
. αύξοντες αριθμοί είναι οι παρακάτω:
αύξοντες αριθμοί είναι οι παρακάτω: 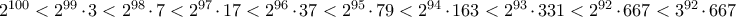
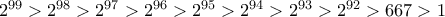
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες