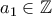 . Ορίζουμε αναδρομικά
. Ορίζουμε αναδρομικά 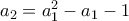 ,
,  ,
,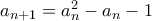 . Να αποδειχθεί ότι ο
. Να αποδειχθεί ότι ο  και ο
και ο  είναι σχετικά πρώτοι.
είναι σχετικά πρώτοι.Συντονιστές: cretanman, silouan, rek2
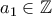 . Ορίζουμε αναδρομικά
. Ορίζουμε αναδρομικά 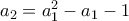 ,
,  ,
,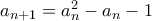 . Να αποδειχθεί ότι ο
. Να αποδειχθεί ότι ο  και ο
και ο  είναι σχετικά πρώτοι.
είναι σχετικά πρώτοι. ένας πρώτος που διαιρεί το
ένας πρώτος που διαιρεί το 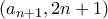 . Προφανώς
. Προφανώς  . Αν ο
. Αν ο  διαιρεί κάποιο
διαιρεί κάποιο  με index
με index 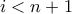 τότε με παρατήρηση προκύπτει ότι για κάθε
τότε με παρατήρηση προκύπτει ότι για κάθε 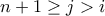
 άτοπο. Άρα το
άτοπο. Άρα το  δεν διαιρεί κανένα άλλο όρο. Από την άλλη αυτό σημαίνει πως
δεν διαιρεί κανένα άλλο όρο. Από την άλλη αυτό σημαίνει πως 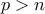 αφού διαφορετικά τα υπόλοιπα έρχονται από pigy σε κύκλους και άρα το
αφού διαφορετικά τα υπόλοιπα έρχονται από pigy σε κύκλους και άρα το  θα είχε ξαναπροκύψει, άτοπο. Επομένως αφού
θα είχε ξαναπροκύψει, άτοπο. Επομένως αφού 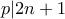 πρέπει αναγκαστικά
πρέπει αναγκαστικά 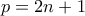 και όλα τα
και όλα τα 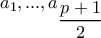 να δίνουν διαφορετικά υπόλοιπα
να δίνουν διαφορετικά υπόλοιπα  και τα
και τα  ,
,  να μην είναι σε αυτά που είναι άτοπο αφού το πλήθος των υπολοίπων που λαμβάνει η παράσταση
να μην είναι σε αυτά που είναι άτοπο αφού το πλήθος των υπολοίπων που λαμβάνει η παράσταση  είναι ίσο με το πλήθος των τετραγωνικών residues + 1 (όταν μηδενίζεται το συμπληρωμένο τετράγωνο) δηλαδή
είναι ίσο με το πλήθος των τετραγωνικών residues + 1 (όταν μηδενίζεται το συμπληρωμένο τετράγωνο) δηλαδή  όμως στερούμαστε την
όμως στερούμαστε την  και την
και την  (προφανές) άρα στους
(προφανές) άρα στους 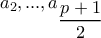 αναγκαστικά δυο θα είναι ίσοι
αναγκαστικά δυο θα είναι ίσοι  άτοπο από πριν.
άτοπο από πριν.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες