Πρόβλημα Γεωμετρίας

[S.E.Louridas]

Καλημέρα καλημέρα.
Επειδή η θεματολογία εκτός των άλλων πρέπει να εμπνέει, αφού από μόνο του το «ψυχρό» δίπολο Άσκηση – Λύση δεν λέει κάτι αν δεν αφήσει την άχλη του θαυμασμού και της προσπάθειας για επιπλέον «κατάκτηση». Εμείς εμπνευστήκαμε από το όμορφο πρόβλημα Γεωμετρίας του διαγωνισμού ΕΥΚΛΕΙΔΗΣ της Γ' Λυκείου και μοιραζόμαστε προτείνοντας στην εδώ μαθηματική μας παρέα το πρόβλημα - γενίκευση που ακολουθεί:

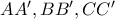Δίνεται τρίγωνο και οι σεβιανές του που τέμνονται σε εσωτερικό του σημείο Θεωρούμε τα εσωτερικά σημεία των 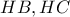αντίστοιχα, τέτοια ώστε η ευθεία να είναι παράλληλη στην Έστω ότι η ευθεία τέμνει τις στα σημεία αντίστοιχα. Αν είναι το σημείο τομής των 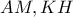και το σημείο τομής των 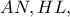να εξετάσετε αν η είναι παράλληλη της

hide: στη θέση της φράσης: στο εσωτερικό του σημείο , τοποθετήθηκε η φράση: σε εσωτερικό του σημείο

[vittasko]

ΕΜΦΑΝΙΣΗ ΚΕΙΜΕΝΟΥ

Το ίδιο πρόβλημα πρότεινε αλλού ο Θανάσης Γακόπουλος και είναι ανεξάρτητο από τις σεβιανές . Αναφέρεται μόνο σε τυχόν σημείο στο εσωτερικό δοσμένου τριγώνου

Ο Θανάσης πρότεινε επίσης και μία άλλη επέκταση του προβλήματος της ΕΜΕ. Θα επανέλθω αργότερα με λεπτομέρειες αν δεν απαντηθεί.

Κώστας Βήττας.

[S.E.Louridas]

όπως τέθηκε εδώ (

Δίνεται τρίγωνο και οι σεβιανές του που τέμνονται σε εσωτερικό του σημείο Θεωρούμε τα εσωτερικά σημεία των αντίστοιχα, τέτοια ώστε η ευθεία να είναι παράλληλη στην Έστω ότι η ευθεία τέμνει τις στα σημεία αντίστοιχα. Αν είναι το σημείο τομής των και το σημείο τομής των να εξετάσετε αν η είναι παράλληλη της

είναι ένας ύμνος στην βασική μετρική ιδιότητα πλήρους τετράπλευρου, ότι δηλαδή κάθε διαγώνιος ενός πλήρους τετράπλευρου διαιρείται αρμονικά από τις άλλες διαγώνιους του.

edit: Άρση της απόκρυψης

[S.E.Louridas]

Δίνεται τρίγωνο και οι σεβιανές του που τέμνονται σε εσωτερικό του σημείο Θεωρούμε τα εσωτερικά σημεία των αντίστοιχα, τέτοια ώστε η ευθεία να είναι παράλληλη στην Έστω ότι η ευθεία τέμνει τις στα σημεία αντίστοιχα. Αν είναι το σημείο τομής των και το σημείο τομής των να εξετάσετε αν η είναι παράλληλη της

Επανέρχομαι τελικά με την ημέτερη διαπραγμάτευση.

Αν είναι το αρμονικό συζυγές του ως προς τα 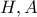, τότε οι ευθείες που ορίζονται από τις διαγώνιες
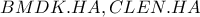των πλήρων τετράπλευρων αντίστοιχα διέρχονται από το λόγω
του βασικού θεωρήματος «κάθε διαγώνιος πλήρους τετράπλευρου διαιρείται αρμονικά από τις άλλες διαγώνιους του».
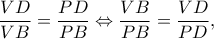Έτσι παίρνουμε: ομοίως έχουμε: 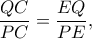οπότε προκύπτει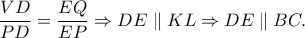

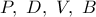π.τ..png (82.3 KiB) Προβλήθηκε 465 φορές

[vittasko]

Δείτε Εδώ απόδειξη του ζητούμενου, ως άμεση εφαρμογή του Θεωρήματος Μενελάου.

Κώστας Βήττας

[achilleas]

Δείτε Εδώ απόδειξη του ζητούμενου, ως άμεση εφαρμογή του Θεωρήματος Μενελάου.

Κώστας Βήττας

Στο παρόμοιο link είχα σχολιάσει επισυνάπτοντας τον τρίτο τρόπο των επίσημων ενδεικτικών λύσεων της ΕΜΕ, καταδεικνύοντας ότι η γενίκευση αυτή είχε εξεταστεί από την επιτροπή διαγωνισμών της ΕΜΕ.

[vittasko]

Αν είναι το αρμονικό συζυγές του ως προς τα , τότε οι ευθείες που ορίζονται από τις διαγώνιες
των πλήρων τετράπλευρων αντίστοιχα διέρχονται από το λόγω
του βασικού θεωρήματος «κάθε διαγώνιος πλήρους τετράπλευρου διαιρείται αρμονικά από τις άλλες διαγώνιους του».

Από εδώ προκύπτει άμεσα το ζητούμενο αφού οι σημειοσειρές και 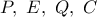είναι αρμονικές και ισχύει .

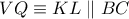Για τυχούσα τέμνουσα δηλαδή, οι ευθείες 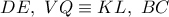συντρέχουν, λόγω των ως άνω αρμονικών σημειοσειρών.

Κώστας Βήττας.

[S.E.Louridas]

Δείτε Εδώ απόδειξη του ζητούμενου, ως άμεση εφαρμογή του Θεωρήματος Μενελάου.

Κώστας Βήττας

Στο παρόμοιο link είχα σχολιάσει επισυνάπτοντας τον τρίτο τρόπο των επίσημων ενδεικτικών λύσεων της ΕΜΕ, καταδεικνύοντας ότι η γενίκευση αυτή είχε εξεταστεί από την επιτροπή διαγωνισμών της ΕΜΕ.

Καταρχάς οι παρεμβάσεις των Άριστων Αχιλλέα και Κώστα είναι ... επίσης άριστες, έστω και αν η γενίκευση που παρέθεσα είναι εύκολο πρόβλημα για διαγωνισμούς. Το έκανα για καθαρά λόγους προβληματισμού ειδικά των διαγωνιζόμενων. Επιτρέψτε μου όμως, και επειδή γνωρίζω την αξία ως κατασκευαστών μελών της επιτροπής διαγωνισμών, να θεωρώ ότι δεν μπορεί να γνώριζαν την παραπάνω γενίκευση (και καλώς) καθότι δεν είναι δυνατόν ενσυνείδητα να θέτουν (κάνω μία παράλληλη κατανοητή τοποθέτηση) πρόβλημα π.χ. του τύπου: Αποδείξτε ότι οι διχοτόμοι ισόπλευρου τριγώνου συντρέχουν (αφού γνωρίζουμε ότι αυτό συμβαίνει σχεδόν άμεσα σε τυχόν τρίγωνο) τουλάχιστον σε περιβάλλον Διαγωνιστικών Μαθηματικών όπου ρόλο παίζει η διδακτέα και όχι η διδαχθείσα ύλη (δηλαδή επιβραβεύεται και ο διαγωνιζόμενος που έχει "ψαχτεί" και γνωρίζει παραπάνω πράγματα για και τα καταθέτει). Για παράδειγμα αν κάποιος μαθητής διαγωνιζόμενος της Β ΛΥΚΕΙΟΥ αποδείξει μία ανισότητα υπό συνθήκη με βάση την μέθοδο απόδειξης μέσω των τελεστών Lagrange αυτή γίνεται απόλυτα αποδεκτή. Θεωρώ λοιπόν ότι οι κατασκευαστές προβλημάτων για τέτοιους διαγωνισμούς θα πρέπει να λαμβάνουν σοβαρά υπόψη την άποψη που εξέφρασα όχι ως δική μου μόνο άποψη αλλά ως άποψη για την κατασκευή προβλημάτων τέτοιου επιπέδου, και γνωρίζω καλά ότι την λαμβάνουν σοβαρά υπόψη και την εφαρμόζουν.

[achilleas]

Σωτήρη, τυγχάνει να γνωρίζω πολύ καλά ότι γνώριζαν τη γενίκευση στην οποία παραπέμπει ο Κώστας παραπάνω με χρήση του Θ. Μενελάου, γι'αυτό και υπήρχε ο 3ος τρόπος λύσεων. Οι ενδεικτικές λύσεις ετοιμάστηκαν πριν την ημέρα του διαγωνισμού.

Η επιλογή ενός απλούστερου προβλήματος για το διαγωνισμό δεν έγινε από άγνοια της γενίκευσης.

Απλά, ως πρόβλημα του διαγωνισμού τέθηκε το πρόβλημα με ορθόκεντρο, για ευνόητους λόγους, και η λύση που αναμένονταν από τους διαγωνιζόμενους ήταν η στοιχειώδης με τον 1ο τρόπο.


Φιλικά,

Αχιλλέας

[S.E.Louridas]

Σωτήρη, τυγχάνει να γνωρίζω πολύ καλά ότι γνώριζαν τη γενίκευση στην οποία παραπέμπει ο Κώστας παραπάνω με χρήση του Θ. Μενελάου, γι'αυτό και υπήρχε ο 3ος τρόπος λύσεων. Οι ενδεικτικές λύσεις ετοιμάστηκαν πριν την ημέρα του διαγωνισμού.

Η επιλογή ενός απλούστερου προβλήματος για το διαγωνισμό δεν έγινε από άγνοια της γενίκευσης.

Απλά, ως πρόβλημα του διαγωνισμού τέθηκε το πρόβλημα με ορθόκεντρο, για ευνόητους λόγους, και η λύση που αναμένονταν από τους διαγωνιζόμενους ήταν η στοιχειώδης με τον 1ο τρόπο.


Φιλικά,

Αχιλλέας

Καλώς Αχιλλέα δεν έχω λόγους να αμφιβάλλω αφού το πιστοποιείς εσύ (ότι δηλαδή γνώριζε ο θεματοδότης εκ των προτέρων τη γενίκευση, αν και η γνώση ή όχι της γενίκευσης δεν σημαίνει και κάτι για την ποιότητα του κατασκευαστή του θέματος αυτού). Έτσι ή αλλιώς είναι πολύ ωραίο πρόβλημα για τον διαγωνισμό ΕΥΚΛΕΙΔΗΣ. Καλή συνέχεια στην προσπάθεια της Άξιας πράγματι επιτροπής των διαγωνισμών (τόσο του πυρήνα της όσο και της διευρυμένης) .