achilleas έγραψε: ↑Παρ Ιούλ 28, 2023 11:22 pm
Έστω

ένα τρίγωνο με έγκεντρο

τέτοιο ώστε
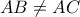
. Έστω

το σημείο τομής των ευθειών

και

. Έστω

το σημείο στο ευθύγραμμο τμήμα

τέτοιο ώστε

. Ομοίως, έστω

το σημείο στο ευθύγραμμο τμήμα

τέτοιο ώστε

. Έστω
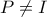
το δεύτερο σημείο τομής των περιγεγραμμένων κύκλων των τριγώνων
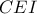
και
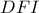
. Ομοίως, έστω
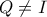
το δεύτερο σημείο τομής των περιγεγραμμένων κύκλων των τριγώνων
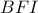
και
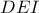
. Να δειθχεί ότι η

είναι κάθετη στη

.
Φιλικά,
Αχιλλέας
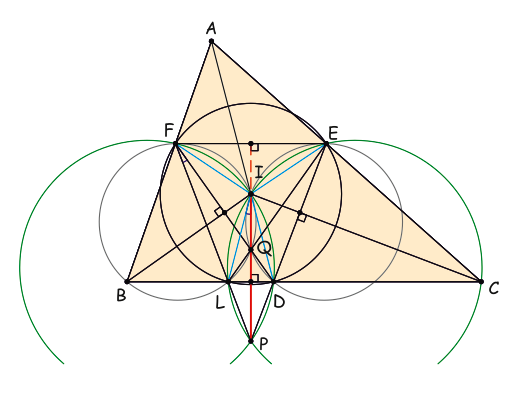
Προφανώς από κατασκευής
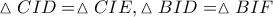
(κριτήριο Π – Γ – Π (από ισότητα τμημάτων και διχοτόμους) και συνεπώς τα τετράπλευρα
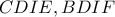
είναι «χαρταετοί» οπότε
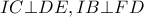
και
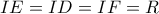
και ας είναι

το σημείο τομής του κύκλου
με την

(προφανώς
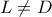
αφού
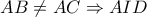
όχι κάθετη στην

)
Είναι
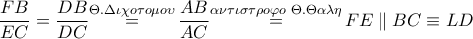
άρα το εγγεγραμμένο στον κύκλο
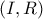
τετράπλευρο
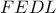
είναι ισοσκελές τραπέζιο και αν
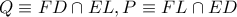
τότε (γνωστή πρόταση (από συμμετρίες))
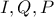
συνευθειακά και
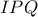
μεσοκάθετη στις βάσεις του
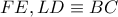
Τότε
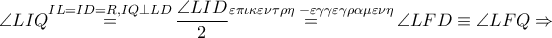
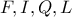
ομοκυκλικά και επίσης
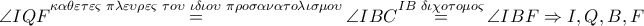
ομοκυκλικά
Από τις δύο αυτές ομοκυκλικές τετράδες με τρία κοινά σημεία προκύπτει ότι
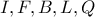
ομοκυκλικά και συνεπώς το

είναι σημείο του κύκλου
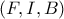
- κάθετες ευθείες.png (46.55 KiB) Προβλήθηκε 582 φορές
Επίσης
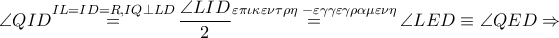
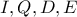
ομοκυκλικά και συνεπώς το

είναι σημείο του κύκλου
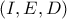
,άρα το

είναι το δεύτερο (εκτός του

) σημείο τομής των κύκλων
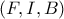
και
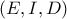
Με ακριβώς όμοιο τρόπο προκύπτει ότι

είναι το δεύτερο (εκτός του

) σημείο τομής των κύκλων
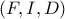
και
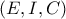
Τελικά
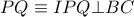
και το ζητούμενο έχει αποδειχθεί.
 ένα τρίγωνο με έγκεντρο
ένα τρίγωνο με έγκεντρο  τέτοιο ώστε
τέτοιο ώστε 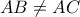 . Έστω
. Έστω  το σημείο τομής των ευθειών
το σημείο τομής των ευθειών  και
και  . Έστω
. Έστω  το σημείο στο ευθύγραμμο τμήμα
το σημείο στο ευθύγραμμο τμήμα  τέτοιο ώστε
τέτοιο ώστε  . Ομοίως, έστω
. Ομοίως, έστω  το σημείο στο ευθύγραμμο τμήμα
το σημείο στο ευθύγραμμο τμήμα  τέτοιο ώστε
τέτοιο ώστε  . Έστω
. Έστω 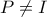 το δεύτερο σημείο τομής των περιγεγραμμένων κύκλων των τριγώνων
το δεύτερο σημείο τομής των περιγεγραμμένων κύκλων των τριγώνων 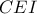 και
και 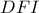 . Ομοίως, έστω
. Ομοίως, έστω 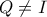 το δεύτερο σημείο τομής των περιγεγραμμένων κύκλων των τριγώνων
το δεύτερο σημείο τομής των περιγεγραμμένων κύκλων των τριγώνων 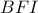 και
και 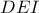 . Να δειθχεί ότι η
. Να δειθχεί ότι η  είναι κάθετη στη
είναι κάθετη στη  .
.
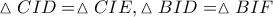 (κριτήριο Π – Γ – Π (από ισότητα τμημάτων και διχοτόμους) και συνεπώς τα τετράπλευρα
(κριτήριο Π – Γ – Π (από ισότητα τμημάτων και διχοτόμους) και συνεπώς τα τετράπλευρα 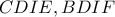 είναι «χαρταετοί» οπότε
είναι «χαρταετοί» οπότε 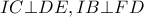 και
και 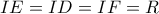 και ας είναι
και ας είναι  το σημείο τομής του κύκλου
το σημείο τομής του κύκλου 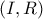 με την
με την 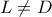 αφού
αφού 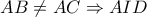 όχι κάθετη στην
όχι κάθετη στην 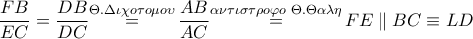 άρα το εγγεγραμμένο στον κύκλο
άρα το εγγεγραμμένο στον κύκλο  είναι ισοσκελές τραπέζιο και αν
είναι ισοσκελές τραπέζιο και αν 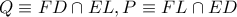 τότε (γνωστή πρόταση (από συμμετρίες))
τότε (γνωστή πρόταση (από συμμετρίες)) 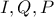 συνευθειακά και
συνευθειακά και 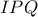 μεσοκάθετη στις βάσεις του
μεσοκάθετη στις βάσεις του 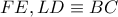
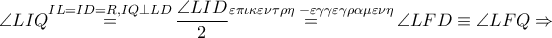
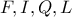 ομοκυκλικά και επίσης
ομοκυκλικά και επίσης 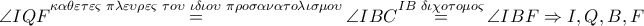 ομοκυκλικά
ομοκυκλικά 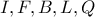 ομοκυκλικά και συνεπώς το
ομοκυκλικά και συνεπώς το  είναι σημείο του κύκλου
είναι σημείο του κύκλου 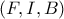
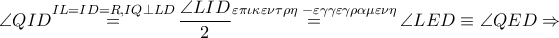
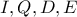 ομοκυκλικά και συνεπώς το
ομοκυκλικά και συνεπώς το 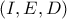 ,άρα το
,άρα το 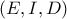
 είναι το δεύτερο (εκτός του
είναι το δεύτερο (εκτός του 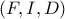 και
και 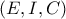
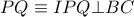 και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί.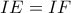 και είναι
και είναι 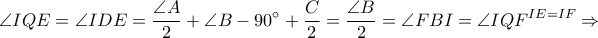
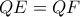
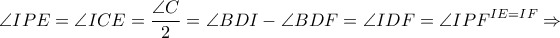

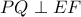 Όμως , είναι
Όμως , είναι 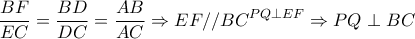 όπως θέλαμε.
όπως θέλαμε.