Αναδιατυπώνουμε τα δοσμένα στοιχεία της εκφώνησης, για ελάφρυνση του σχήματος.
Έτσι, επί ευθείας

, δίνεται η αρμονική σημειοσειρά

και ας είναι

, τα μεσα των τμημάτων

, αντιστοίχως. Έστω

, το σημείο επί της δια του

κάθετης ευθείας επί την

, ώστε να είναι

και έστω το σημείο

, ώστε να είναι

.
Θα αποδειχθεί ότι ο κύκλος με κέντρο το σημείο

και ακτίνα

, εφάπτεται και του κύκλου

με διάμετρο

.

Θεωρούμε την Αντιστροφή με πόλο το σημείο

και δύναμη

η οποία αντιστρέφει τον κύκλο

στην εφαπτομένη του

στο σημείο

και ας είναι

, το αντίστροφο του σημείου

στην ίδια Αντιστροφή.
Για την κατασκευή του σημείου

ως άνω, γράφουμε τον κύκλο

με κέντρο το σημείο

και ακτίνα

( = ο κύκλος της Αντιστροφής ) και ορίζουμε ως

, το σημείο τομής του

, από την δια του σημείου

κάθετη ευθεία επί την

. Η δια του σημείου

κάθετη ευθεία επί την

, τέμνει την ευθεία

στο σημείο

αντίστροφο του

, γιατί ισχύει

, από το ορθογώνιο τρίγωνο

με

.
Έστω

, το σημείο τομής της ευθείας

, από την δια του σημείου

κάθετη ευθεία επί την

.
Ο κύκλος έστω

, με κέντρο το σημείο

και ακτίνα

, είναι αντίστροφος του κύκλου

στην ως άνω Αντιστροφή, λόγω της ομοιοθεσίας των δύο κύκλων ως προς εξωτερικό κέντρο ομοιοθεσίας τους, τον πόλο της αντιστροφής

.
Επομένως, για να εφάπτεται ο κύκλος

στον κύκλο

που είναι το ζητούμενο, αρκεί να αποδειχθεί ότι ο αντίστροφός του κύκλος

, εφάπτεται στην ευθεία

που είναι η εικόνα ( = αντίστροφο σχήμα ) του κύκλου

στην ίδια Αντιστροφή.
Αρκεί δηλαδή να αποδειχθεί ότι ισχύει


- Κύκλος εφάπτεται ημικυκλίου λόγω αρμονικότητας.
- f 185_t 69010(a).PNG (43.05 KiB) Προβλήθηκε 624 φορές

Έστω τα σημεία

και

και έχουμε

από το ορθογώνιο τρίγωνο

με




αντίστροφα σημεία

Από

και


και άρα, το τετράπλευρο

είναι εγγράψιμο σε κύκλο έστω

και επομένως έχουμε

Από

και

, λόγω του εγραψίμου

, προκύπτει


Από

και


λόγω των ομοίων ορθογωνίων τριγώνων

.
Από


Από
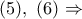


Σύμφωνα με το παρακάτω
Λήμμα, έχουμε

Από


και το ισοδύναμο ζητούμενο έχει αποδειχθεί.
ΛΗΜΜΑ. Eπί ευθείας  , δίνεται η αρμονική σημειοσειρά
, δίνεται η αρμονική σημειοσειρά  και ας είναι
και ας είναι  , τα μεσα των τμημάτων
, τα μεσα των τμημάτων  , αντιστοίχως. Έστω
, αντιστοίχως. Έστω  , το σημείο επί της δια του
, το σημείο επί της δια του  κάθετης ευθείας επί την
κάθετης ευθείας επί την  , ώστε να είναι
, ώστε να είναι  και έστω το σημείο
και έστω το σημείο  , ώστε να είναι
, ώστε να είναι  και ας είναι
και ας είναι  , το σημείο τομής της ευθείας
, το σημείο τομής της ευθείας  , από την δια του σημείου
, από την δια του σημείου  κάθετη ευθεία επί την
κάθετη ευθεία επί την  . Αποδείξτε ότι
. Αποδείξτε ότι 
.
Κώστας Βήττας.
ΥΓ. Θα βάλω αργότερα απόδειξη που έχω υπόψη μου, το ως άνω
Λήμμα.
 δίνεται η σημειοσειρά
δίνεται η σημειοσειρά  και έστω τα ημικύκλια
και έστω τα ημικύκλια  , με διάμετρο
, με διάμετρο  , αντιστοίχως. Έστω
, αντιστοίχως. Έστω  , το μέσον του ημικυκίου
, το μέσον του ημικυκίου  και
και  η εφαπτομένη του και
η εφαπτομένη του και  , η προβολή του σημείου
, η προβολή του σημείου  επί της
επί της  . Αποδείξτε ότι ο κύκλος έστω
. Αποδείξτε ότι ο κύκλος έστω  , με κέντρο το σημείο
, με κέντρο το σημείο  και ακτίνα
και ακτίνα  , εφάπτεται και του ημικυκλίου
, εφάπτεται και του ημικυκλίου  .
. Αφιερώνεται σε ένδειξη τιμής, στον Ευθύμη Αλεξίου. (*)
Κώστας Βήττας.
Αφιερώνεται σε ένδειξη τιμής, στον Ευθύμη Αλεξίου. (*)
Κώστας Βήττας. ταυτίζεται με την Πολική ευθεία του σημείου
ταυτίζεται με την Πολική ευθεία του σημείου  ως προς τον κύκλο
ως προς τον κύκλο  και επομένως, η σημειοσειρά
και επομένως, η σημειοσειρά  , είναι αρμονική. Έχω υπόψη μου μία μακροσκελή απόδειξη που δεν ταιριάζει με την απλότητα της εκφώνησης και προσδοκώ σε μία συντομότερη λύση, με λίγα "κουνήματα", αν γίνεται.
, είναι αρμονική. Έχω υπόψη μου μία μακροσκελή απόδειξη που δεν ταιριάζει με την απλότητα της εκφώνησης και προσδοκώ σε μία συντομότερη λύση, με λίγα "κουνήματα", αν γίνεται. 
 . Επειδή η τετράδα :
. Επειδή η τετράδα :  είναι ως γνωστό αρμονική προκύπτει :
είναι ως γνωστό αρμονική προκύπτει :  εύκολα μετά ( απλές πράξεις Γυμνασίου)
εύκολα μετά ( απλές πράξεις Γυμνασίου)
 προκύπτει η ακτίνα
προκύπτει η ακτίνα 
 με πόλο το
με πόλο το  και δύναμη αντιστροφής
και δύναμη αντιστροφής  και μετασχηματίζεται σε ευθεία
και μετασχηματίζεται σε ευθεία  κάθετη στην
κάθετη στην  σε σημείο
σε σημείο 
 ότι :
ότι :  η ευθεία
η ευθεία  .
. είναι ισοσκελές ορθογώνιο
είναι ισοσκελές ορθογώνιο  είναι στην ίδια ευθεία με το
είναι στην ίδια ευθεία με το  σημείο του ημικυκλίου
σημείο του ημικυκλίου  , της ευθείας
, της ευθείας  ομοιόθετο του
ομοιόθετο του  , αντίστροφο του
, αντίστροφο του  και το ζητούμενο έπεται, αφού αποδεικνύεται ότι ο
και το ζητούμενο έπεται, αφού αποδεικνύεται ότι ο  αλλά συνεχίζω
αλλά συνεχίζω
 και με Π.Θ στο
και με Π.Θ στο 
 απ' όπου παίρνω
απ' όπου παίρνω και εύκολα τώρα διαπιστώνω ότι
και εύκολα τώρα διαπιστώνω ότι 
 , τα μέσα των τμημάτων
, τα μέσα των τμημάτων  και όπου το ζητούμενο είναι να αποδειχθεί ότι ισχύει
και όπου το ζητούμενο είναι να αποδειχθεί ότι ισχύει  , με
, με  και
και  .
. σταθερά σημεία και μεταβλητά τα
σταθερά σημεία και μεταβλητά τα  , αλλά πάντοτε η σημειοσειρά
, αλλά πάντοτε η σημειοσειρά  σταθερό και το κέντρο του
σταθερό και το κέντρο του  κινείται σε Παραβολή χορδής
κινείται σε Παραβολή χορδής  το οποίο ταυτίζεται με την εστία της.
το οποίο ταυτίζεται με την εστία της. κάθετης ευθείας επί την
κάθετης ευθείας επί την  και έστω το σημείο
και έστω το σημείο  στο σημείο
στο σημείο  , το αντίστροφο του σημείου
, το αντίστροφο του σημείου  με κέντρο το σημείο
με κέντρο το σημείο  ( = ο κύκλος της Αντιστροφής ) και ορίζουμε ως
( = ο κύκλος της Αντιστροφής ) και ορίζουμε ως  , τέμνει την ευθεία
, τέμνει την ευθεία  , από το ορθογώνιο τρίγωνο
, από το ορθογώνιο τρίγωνο  με
με  .
. , το σημείο τομής της ευθείας
, το σημείο τομής της ευθείας  , από την δια του σημείου
, από την δια του σημείου  , είναι αντίστροφος του κύκλου
, είναι αντίστροφος του κύκλου 
 και
και  και έχουμε
και έχουμε 
 με
με 


 αντίστροφα σημεία
αντίστροφα σημεία 
 και
και 
 και άρα, το τετράπλευρο
και άρα, το τετράπλευρο 
 και επομένως έχουμε
και επομένως έχουμε 
 και
και  , λόγω του εγραψίμου
, λόγω του εγραψίμου  , προκύπτει
, προκύπτει 

 και
και 
 λόγω των ομοίων ορθογωνίων τριγώνων
λόγω των ομοίων ορθογωνίων τριγώνων  .
.

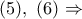




 και το ισοδύναμο ζητούμενο έχει αποδειχθεί.
και το ισοδύναμο ζητούμενο έχει αποδειχθεί. , το σημείο τομής της ευθείας
, το σημείο τομής της ευθείας 
 και από
και από 

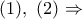


 , αρκεί
, αρκεί  αρκεί
αρκεί  αρκεί
αρκεί 
 όμως, ισχύει λόγω της δοσμένης αρμονικής σημειοσειράς
όμως, ισχύει λόγω της δοσμένης αρμονικής σημειοσειράς  (*) και το
(*) και το