Για φυσικό
 ορίζουμε το
ορίζουμε το  ως τον μέγιστο πρώτο διαιρέτη του
ως τον μέγιστο πρώτο διαιρέτη του  .
.Έστω η ακολουθία
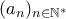 με
με 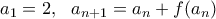 .
.Να βρεθεί ο μέγιστος
 με
με 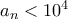 .
.Συντονιστές: cretanman, silouan, rek2
 ορίζουμε το
ορίζουμε το  ως τον μέγιστο πρώτο διαιρέτη του
ως τον μέγιστο πρώτο διαιρέτη του  .
.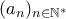 με
με 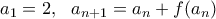 .
. με
με 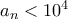 .
. , υπάρχει αντίστοιχος ίσος όρος της ακολουθίας.
, υπάρχει αντίστοιχος ίσος όρος της ακολουθίας. η ακολουθία των πρώτων αριθμών.
η ακολουθία των πρώτων αριθμών.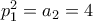
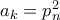 , θα δείξω ότι
, θα δείξω ότι 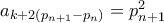 .
.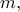 με
με 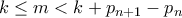 , είναι
, είναι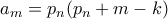 .
.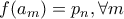 .
.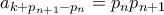 .
.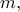 με
με 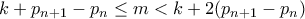 , είναι
, είναι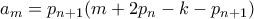 .
.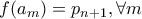 .
.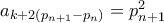 .
.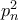 στο
στο 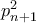 , προχωράμε κατά
, προχωράμε κατά 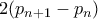
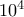 είναι το
είναι το 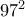 .
.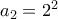 στο
στο 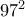 , προχωρούμε κατά
, προχωρούμε κατά 
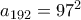
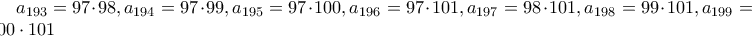
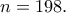
 δεν έχουμε
δεν έχουμε  (διορθώθηκε).
(διορθώθηκε).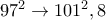 όροι μπροστά). Έκανα τη διόρθωση.Ελπίζω να είναι σωστό τώρα.
όροι μπροστά). Έκανα τη διόρθωση.Ελπίζω να είναι σωστό τώρα.Πρακτικά ίδια ιδέα:
 υπάρχουν
υπάρχουν 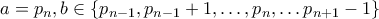 ,τέτοια ώστε:
,τέτοια ώστε: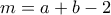 και
και 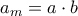 .
.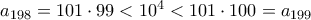 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες