Να βρείτε όλα τα ζεύγη θετικών ακεραίων
 που είναι τέτοια ώστε
που είναι τέτοια ώστε  .
.Συντονιστές: cretanman, silouan, rek2
 που είναι τέτοια ώστε
που είναι τέτοια ώστε  .
. παίρνουμε
παίρνουμε  . Για
. Για  παίρνουμε
παίρνουμε  κι έτσι
κι έτσι  και λόγω του ότι
και λόγω του ότι  , οι δυνάμεις
, οι δυνάμεις  επαναλαμβάνονται κάθε
επαναλαμβάνονται κάθε  κι έτσι διαιρώντας τον εκθέτη
κι έτσι διαιρώντας τον εκθέτη  με το
με το  , βρίσκουμε ότι για να ισχύει η
, βρίσκουμε ότι για να ισχύει η  πρέπει
πρέπει  , έστω
, έστω  . Αντικαθιστώντας στην αρχική και παίρνοντας
. Αντικαθιστώντας στην αρχική και παίρνοντας  (λόγω του μικρού θεωρήματος του Fermat έχουμε
(λόγω του μικρού θεωρήματος του Fermat έχουμε  ) παίρνουμε τελικά
) παίρνουμε τελικά  και λόγω του ότι
και λόγω του ότι  , άρα οι μόνες τιμές για το
, άρα οι μόνες τιμές για το  που αρκεί να δοκιμάσουμε είναι οι
που αρκεί να δοκιμάσουμε είναι οι  για καμία από τις οποίες δεν ισχύει η
για καμία από τις οποίες δεν ισχύει η  .
. .
.Μπορεί κάποιος να μου εξηγήσει το σημείο αυτό ?-cretanman έγραψε: ↑Τετ Μάιος 01, 2019 9:50 pmΔύσκολη!
Γιαπαίρνουμε
. Για
παίρνουμε
κι έτσι
και λόγω του ότι
, οι δυνάμεις
επαναλαμβάνονται κάθε
κι έτσι διαιρώντας τον εκθέτη
με το
, βρίσκουμε ότι για να ισχύει η
πρέπει
, έστω
. Αντικαθιστώντας στην αρχική και παίρνοντας
(λόγω του μικρού θεωρήματος του Fermat έχουμε
) παίρνουμε τελικά
και λόγω του ότι
, άρα οι μόνες τιμές για το
που αρκεί να δοκιμάσουμε είναι οι
για καμία από τις οποίες δεν ισχύει η
.
Άρα μοναδική λύση η.
Αλέξανδρος

Καλημέρα! Εάν
 ένας ακέραιος και
ένας ακέραιος και  ένας ακέραιος πρώτος προς το
ένας ακέραιος πρώτος προς το  , τότε το
, τότε το  ("τάξη του
("τάξη του  " στα ελληνικά) ορίζεται ως ο ελάχιστος θετικός ακέραιος
" στα ελληνικά) ορίζεται ως ο ελάχιστος θετικός ακέραιος  ώστε
ώστε  .
.  ώστε
ώστε  είναι το
είναι το  .
. , αποδεικνύεται σχετικά εύκολα ότι το
, αποδεικνύεται σχετικά εύκολα ότι το  διαιρεί το
διαιρεί το  . Γι'αυτό όταν αναζητούμε την τάξη ενός ακεραίου
. Γι'αυτό όταν αναζητούμε την τάξη ενός ακεραίου  ψάχνουμε πάντα στους διαιρέτες του
ψάχνουμε πάντα στους διαιρέτες του  . Έτσι, αφού
. Έτσι, αφού  άρα η τάξη του
άρα η τάξη του  είναι κάποιος διαιρέτης του
είναι κάποιος διαιρέτης του  και αφού κανένας εκ των δυνάμεων
και αφού κανένας εκ των δυνάμεων  δεν είναι ίσο με
δεν είναι ίσο με  , συμπεραίνουμε ότι
, συμπεραίνουμε ότι 
Θα μπορούσες να βάλεις αναλυτικά τη λύση σου; Η παραπάνω απέχει πάρα πολύ από το να μπορεί να θεωρηθεί ως λύση και σίγουρα δε θα έπαιρνε πάρα ελάχιστες έως καθόλου μονάδες σε επίπεδο διαγωνισμών.
Με
 έχω:
έχω: 
 έχω:
έχω:
 έχω:
έχω:


 έχω :
έχω :
 έχω:
έχω: (όπως πρίν)
(όπως πρίν) έχω:
έχω:

 έχω μοναδική λύση την
έχω μοναδική λύση την 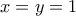
 τότε και
τότε και  :
: έχουμε:
έχουμε:
 έχουμε:
έχουμε:
 τότε και
τότε και 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες