george visvikis έγραψε: ↑Σάβ Απρ 06, 2024 1:57 pm
Ορισμός: Θεωρούμε τετράεδρο

Αν μία τρίεδρη γωνία του, π.χ η τρίεδρη γωνία με κορυφή

είναι τρισορθογώνια, τότε το

ονομάζεται
τρισορθογώνιο τετράεδρο κατά την κορυφή

Τρισορθογώνιο τετράεδρο.png
Δίνεται τρισορθογώνιο τετράεδρο

κατά την κορυφή

Μία μεταβλητή σφαίρα

διέρχεται από τα
σημεία

Αν οι

επανατέμνουν τη σφαίρα στα σημεία

αντίστοιχα και

είναι το βαρύκεντρο του τριγώνου

να δείξετε ότι η

είναι κάθετη στο επίπεδο του τριγώνου

και διέρχεται από το ορθόκεντρό του.
Παρατηρούμε ότι το τετράεδρο

είναι ορθοκεντρικό. Πράγματι τα ύψη του διέρχονται από το ίδιο σημείο

. Άρα, λόγω των ιδιοτήτων των ρθοκεντρικών τετράεδρων, οι απέναντι ακμές του είναι κάθετες μεταξύ τους.
Θα δείξουμε την παρακάτω πρόταση για ορθοκεντρικά τετράεδρα.
Πρόταση 1. Σε ορθοκεντρικό τετράεδρο τα σημεία

( το κέντρο της περιγεγραμμένης σφαίρας, το σημείο τομής των διαμέσων του και το σημείο τομής των υψών του αντίστοιχα) βρίσκονται στην ίδια ευθεία (ευθεία Euler ορθοκεντρικού τετράεδρου) και

είναι το μέσο του
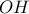
.
Απόδειξη: Έστω

σημείο για το οποίο

. Τότε

και

.
Εφόσον

, τότε θα ισχύει

,

και

. Επομένως

Η τελευταία έκφραση είναι συμμετρική ως προς τα

, άρα θα ισχύει

. Δηλαδή το σημείο

συμπίπτει με το κέντρο της περιγεγραμμένης σφαίρας

, του τετράεδρου

.
Δείξαμε ότι

Από την άλλη

. Από όπου πέρνουμε

Όμως

, οπότε τελικά έχουμε

.

Θα δείξουμε και την παρακάτω πρόταση , γενικά για τετράεδρα.
Πρόταση 2. Φέρουμε σφαίρα που διέρχεται από τις κορυφές

ενός τετράεδρου

η οποία τέμνει τις ακμές

ή τις προεκτάσεις τους στα σημεία

αντίστοιχα. Τότε το επίπεδο

είναι παράλληλο στο εφαπτόμενο επίπεδο στην περιγεγεγραμμένη σφαίρα του

στο σημείο

. Το τρίγωνο

συχνά αναφέρεται και ως
αντιπαράλληλη τομή του τετράεδρου 
ως προς το σημείο

.
Απόδειξη: Θεωρούμε το επίπεδο, που ορίζουν τα σημεία

και έστω

η τομή αυτού του επιπέδου με το εφαπτόμενο επίπεδο στο σημείο

. Από το θεώρημα χορδής και εφαπτομένης έχουμε ότι

.
Από το εγεγραμμένο τετράπλευρο

(στην αρχική μας σφαίρα), έχουμε ότι

. 'Αρα θα ισχύει

. Δηλαδή

.
Ομοίως βρίσκουμε και ότι οι ευθείες

παράλληλες προς το εφαπτόμενο επίπεδο της περιγεγραμμένης σφαίρας του

στο σημείο

. Άρα και το επίπεδο

θα είναι παράληλλο προς αυτό.

Στο πρόβλημά μας τώρα. Εφόσον το

είναι ορθοκεντρικό, από την πρόταση 1 παραπάνω, τo σημεία

, το κέντρο της περιγεγραμμένης σφαίρας

και το ορθόκεντρο

είναι συνευθειακά. 'Αρα η

, ως φορέας της ακτίνας της περιγεγραμμένης σφαίρας του

είναι κάθετη προς το εφαπτόμενο επίπεδο σε αυτή την σφαίρα στο σημείο

.
Από την πρόταση 2 όμως το επίπεδο

είναι η αντιπαράλληλη τομή του τετραέδρου

ως προς το σημείο

, οπότε είναι παράλληλο προς το παραπάνω εφαπτόμενο επίπεδο.
Επομένως η ευθεία

είναι κάθετη και στο επίπεδο


- trisorthogonio_tetraedro.png (123.64 KiB) Προβλήθηκε 325 φορές
 Αν μία τρίεδρη γωνία του, π.χ η τρίεδρη γωνία με κορυφή
Αν μία τρίεδρη γωνία του, π.χ η τρίεδρη γωνία με κορυφή 
 ονομάζεται τρισορθογώνιο τετράεδρο κατά την κορυφή
ονομάζεται τρισορθογώνιο τετράεδρο κατά την κορυφή  Δίνεται τρισορθογώνιο τετράεδρο
Δίνεται τρισορθογώνιο τετράεδρο  κατά την κορυφή
κατά την κορυφή  Μία μεταβλητή σφαίρα
Μία μεταβλητή σφαίρα  διέρχεται από τα
διέρχεται από τα  Αν οι
Αν οι  επανατέμνουν τη σφαίρα στα σημεία
επανατέμνουν τη σφαίρα στα σημεία  αντίστοιχα και
αντίστοιχα και 
 να δείξετε ότι η
να δείξετε ότι η  είναι κάθετη στο επίπεδο του τριγώνου
είναι κάθετη στο επίπεδο του τριγώνου 

 είναι ομοκυκλικά αφού η τομή σφαίρας από επίπεδο (αν υπάρχει και εδώ υπάρχει) είναι κύκλος.
είναι ομοκυκλικά αφού η τομή σφαίρας από επίπεδο (αν υπάρχει και εδώ υπάρχει) είναι κύκλος.  κύκλου που τέμνονται στο
κύκλου που τέμνονται στο  τότε η κάθετη από το
τότε η κάθετη από το  στην
στην  διέρχεται από το μέσο της
διέρχεται από το μέσο της 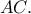
 με την
με την  να είναι κάθετη στο επίπεδο
να είναι κάθετη στο επίπεδο  αφού
αφού 
 Αν ονομάσουμε
Αν ονομάσουμε  το ορθόκεντρο του τριγώνου
το ορθόκεντρο του τριγώνου 
 είναι συνεπίπεδη με το ύψος πλέον
είναι συνεπίπεδη με το ύψος πλέον  και η διάμεσος
και η διάμεσος 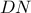 συνεπίππεδη με το ύψος
συνεπίππεδη με το ύψος 
 στην οποία ανήκει η κορυφή
στην οποία ανήκει η κορυφή  . Άρα, λόγω των ιδιοτήτων των ρθοκεντρικών τετράεδρων, οι απέναντι ακμές του είναι κάθετες μεταξύ τους.
. Άρα, λόγω των ιδιοτήτων των ρθοκεντρικών τετράεδρων, οι απέναντι ακμές του είναι κάθετες μεταξύ τους. ( το κέντρο της περιγεγραμμένης σφαίρας, το σημείο τομής των διαμέσων του και το σημείο τομής των υψών του αντίστοιχα) βρίσκονται στην ίδια ευθεία (ευθεία Euler ορθοκεντρικού τετράεδρου) και
( το κέντρο της περιγεγραμμένης σφαίρας, το σημείο τομής των διαμέσων του και το σημείο τομής των υψών του αντίστοιχα) βρίσκονται στην ίδια ευθεία (ευθεία Euler ορθοκεντρικού τετράεδρου) και  είναι το μέσο του
είναι το μέσο του 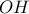 .
. σημείο για το οποίο
σημείο για το οποίο  . Τότε
. Τότε  και
και .
. , τότε θα ισχύει
, τότε θα ισχύει  ,
, και
και  . Επομένως
. Επομένως 
 , άρα θα ισχύει
, άρα θα ισχύει  . Δηλαδή το σημείο
. Δηλαδή το σημείο  , του τετράεδρου
, του τετράεδρου 
 . Από όπου πέρνουμε
. Από όπου πέρνουμε
 , οπότε τελικά έχουμε
, οπότε τελικά έχουμε .
. 
 ενός τετράεδρου
ενός τετράεδρου  ή τις προεκτάσεις τους στα σημεία
ή τις προεκτάσεις τους στα σημεία  αντίστοιχα. Τότε το επίπεδο
αντίστοιχα. Τότε το επίπεδο  είναι παράλληλο στο εφαπτόμενο επίπεδο στην περιγεγεγραμμένη σφαίρα του
είναι παράλληλο στο εφαπτόμενο επίπεδο στην περιγεγεγραμμένη σφαίρα του  και έστω
και έστω  η τομή αυτού του επιπέδου με το εφαπτόμενο επίπεδο στο σημείο
η τομή αυτού του επιπέδου με το εφαπτόμενο επίπεδο στο σημείο  .
.  (στην αρχική μας σφαίρα), έχουμε ότι
(στην αρχική μας σφαίρα), έχουμε ότι  . 'Αρα θα ισχύει
. 'Αρα θα ισχύει  . Δηλαδή
. Δηλαδή  .
. παράλληλες προς το εφαπτόμενο επίπεδο της περιγεγραμμένης σφαίρας του
παράλληλες προς το εφαπτόμενο επίπεδο της περιγεγραμμένης σφαίρας του  , το κέντρο της περιγεγραμμένης σφαίρας
, το κέντρο της περιγεγραμμένης σφαίρας  και το ορθόκεντρο
και το ορθόκεντρο  είναι συνευθειακά. 'Αρα η
είναι συνευθειακά. 'Αρα η  , ως φορέας της ακτίνας της περιγεγραμμένης σφαίρας του
, ως φορέας της ακτίνας της περιγεγραμμένης σφαίρας του  Αν πάρουμε ως σημείο αναφοράς το τρίγωνο
Αν πάρουμε ως σημείο αναφοράς το τρίγωνο  του τριγώνου
του τριγώνου  θα προβάλλεται στο κέντρο
θα προβάλλεται στο κέντρο  του περιγεγραμμένου κύκλου του
του περιγεγραμμένου κύκλου του  Από το θεώρημα Euler στο τρίγωνο
Από το θεώρημα Euler στο τρίγωνο  άρα το κέντρο βάρους
άρα το κέντρο βάρους  στο οποίο επίπεδο ανήκει και το
στο οποίο επίπεδο ανήκει και το 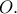 Με ίδιο σκεπτικό θα ανήκει και στο αντίστοιχο επίπεδο
Με ίδιο σκεπτικό θα ανήκει και στο αντίστοιχο επίπεδο  αν πάρουμε σαν βάση το τρίγωνο
αν πάρουμε σαν βάση το τρίγωνο  και απέναντι κορυφή το
και απέναντι κορυφή το  Τα επίπεδα όμως αυτά έχουν ως τομή την ευθεία
Τα επίπεδα όμως αυτά έχουν ως τομή την ευθεία  στην οποία αναγκαστικά θα ανήκει και το σημείο
στην οποία αναγκαστικά θα ανήκει και το σημείο  της
της  με το μέσο
με το μέσο  του ευθύγραμμου τμήματος
του ευθύγραμμου τμήματος 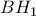 τότε ορίζεται το τρίγωνο
τότε ορίζεται το τρίγωνο  που η πλευρά του
που η πλευρά του  διέρχεται από το μέσο
διέρχεται από το μέσο  του
του  και που οδηγεί στο ότι
και που οδηγεί στο ότι  Είναι βέβαια γνωστό ότι το
Είναι βέβαια γνωστό ότι το 