Βάζω και τη δική μου λύση.

Γιώργο, σ ευχαριστώ!
1ο σκέλος-αρχικό πρόβλημα.
Έχουμε
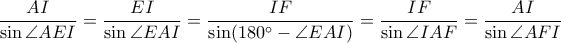
και αφού
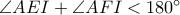
, έχουμε
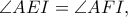
άρα το τετράπλευρο

είναι εγγράψιμο. Έστω
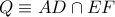
. Το τετράπλευρο
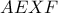
είναι αρμονικό, άρα
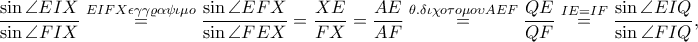
άρα τα σημεία
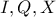
είναι συνευθειακά. Θεωρούμε το μέσο

του

και ως γνωστό, η ευθεία

διέρχεται από το αντιδιαμετρικό

του

ως προς τον περιγεγραμμένο κύκλο του εγγράψιμου τετραπλεύρου

(αφού
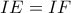
).
Είναι
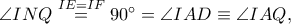
άρα το τετράπλευρο
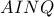
είναι εγγράψιμο. Επιπλέον
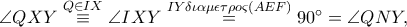
άρα το τετράπλευρο
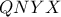
είναι εγγράψιμο. Οι ευθείες
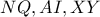
συντρέχουν στο ριζικό κέντρο των κύκλων
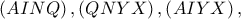
έστω
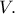
Η

είναι εσωτερική διχοτόμος στο τρίγωνο

και η
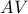
εξωτερική, άρα η δέσμη

είναι αρμονική, επομένως το

είναι το αρμονικό συζυγές του

ως προς τα

και ταυτίζεται με το αρμονικό συζυγές του

ως προς τα

άρα τα σημεία
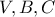
είναι συνευθειακά. Αφού
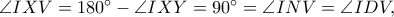
τα σημεία
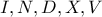
είναι ομοκυκλικά, άρα
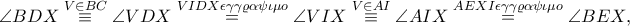
άρα το τετράπλευρο
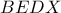
είναι εγγράψιμο και συνεπώς το

είναι το σημείο
Miquel του τριγώνου

ως προς τα σημεία
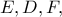
άρα το τετράπλευρο
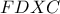
είναι εγγράψιμο. Επομένως
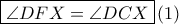
και
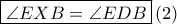
και αφού το

είναι το κέντρο του κύκλου
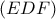
και
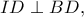
η

εφάπτεται του περιγεγραμμένου κύκλου του τριγώνου
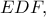
άρα
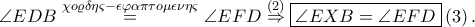
Φέρνουμε την εφαπτομένη στο

του περιγεγραμμένου κύκλου του τριγώνου

και έστω ένα τυχαίο σημείο της

άρα
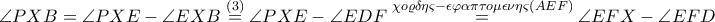
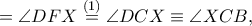
άρα η ευθεία

εφάπτεται του περιγεγραμμένου κύκλου του τριγώνου
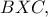
συνεπώς οι περιγεγραμμένοι κύκλοι των τριγώνων

και

δέχονται στο κοινό τους σημείο

κοινή εφαπτομένη, άρα εφάπτονται στο σημείο
 2ο σκέλος- επιπρόσθετο ερώτημα.
2ο σκέλος- επιπρόσθετο ερώτημα.
Έχουμε
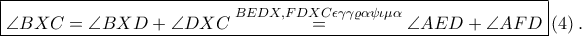
Επιπλέον, το

είναι το περίκεντρο του τριγώνου
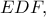
άρα
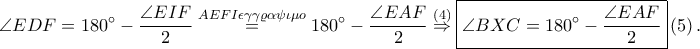
Θεωρούμε το μέσο

του μη κυρτού τόξου της χορδής

του περιγεγραμμένου κύκλου του τριγώνου

άρα
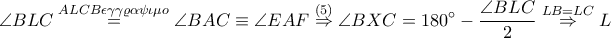
είναι το περίκεντρο του τριγώνου

και αφού οι περιγεγραμμένοι κύκλοι των τριγώνων

και

εφάπτονται, έπεται ότι τα σημεία
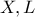
και το περίκεντρο του τριγώνου

είναι συνευθειακά.
Υ.Γ Η λύση του Γιώργου (Κοτσάλη) είναι εξαιρετική. Το πρόβλημα μπορεί να λυθεί και με bashing, αλλά εμείς είμαστε fun της γεωμετρίας και σε όποιον αρέσει.

 με εσωτερική διχοτόμο
με εσωτερική διχοτόμο 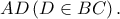 Η κάθετη από το
Η κάθετη από το  στην
στην  τέμνει την εξωτερική διχοτόμο της γωνίας
τέμνει την εξωτερική διχοτόμο της γωνίας  στο σημείο
στο σημείο  και ο κύκλος κέντρου
και ο κύκλος κέντρου  και ακτίνας
και ακτίνας  τέμνει τις πλευρές
τέμνει τις πλευρές  στα σημεία
στα σημεία  αντίστοιχα. Αν η ευθεία της
αντίστοιχα. Αν η ευθεία της  - συμμετροδιαμέσου του τριγώνου
- συμμετροδιαμέσου του τριγώνου  επανατέμνει τον περιγεγραμμένο κύκλο του στο σημείο
επανατέμνει τον περιγεγραμμένο κύκλο του στο σημείο  , να αποδείξετε ότι οι περιγεγραμμένοι κύκλοι των τριγώνων
, να αποδείξετε ότι οι περιγεγραμμένοι κύκλοι των τριγώνων  και
και  εφάπτονται.
εφάπτονται.
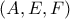 ( μπλε) με πόλο το
( μπλε) με πόλο το 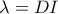 και προκύπτει η ευθεία
και προκύπτει η ευθεία  .
.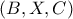 με ίδιο πόλο και ίδια δύναμη και προκύπτει ο κύκλος
με ίδιο πόλο και ίδια δύναμη και προκύπτει ο κύκλος  ( λαχανί επιφάνεια) .
( λαχανί επιφάνεια) .
 , σημείο επαφής της
, σημείο επαφής της  , οπότε οι κύκλοι :
, οπότε οι κύκλοι : 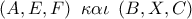 εφάπτονται στο σημείο
εφάπτονται στο σημείο  το μέσο του μεγάλου τόξου
το μέσο του μεγάλου τόξου  του περιγεγραμμένου κύκλου του τριγώνου
του περιγεγραμμένου κύκλου του τριγώνου 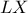 περνάει από το περίκεντρο του τριγώνου
περνάει από το περίκεντρο του τριγώνου 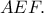
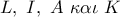 ανήκουν στην ίδια ευθεία .
ανήκουν στην ίδια ευθεία . και το μέσο
και το μέσο  του τόξου
του τόξου  είναι συνευθειακά.
είναι συνευθειακά. η τομή των κάθετων στις
η τομή των κάθετων στις 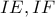 ευθειών που άγονται από τα
ευθειών που άγονται από τα 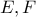 αντίστοιχα τότε
αντίστοιχα τότε 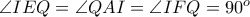 , απ' όπου τα τετράπλευρα
, απ' όπου τα τετράπλευρα 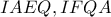 είναι εγγράψιμα, και τα
είναι εγγράψιμα, και τα 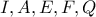 είναι ομοκυκλικά στον κύκλο διαμέτρου
είναι ομοκυκλικά στον κύκλο διαμέτρου  .
. και κύκλος
και κύκλος 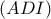 έχει κέντρο το μέσο της
έχει κέντρο το μέσο της  (αφού
(αφού 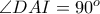 ), άρα εφάπτεται της
), άρα εφάπτεται της 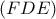 , οπότε ο ριζικός τους άξονας είναι η
, οπότε ο ριζικός τους άξονας είναι η 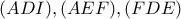 , έχουμε ότι οι ανά δύο ριζικοί τους άξονες συντρέχουν, άρα οι
, έχουμε ότι οι ανά δύο ριζικοί τους άξονες συντρέχουν, άρα οι 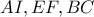 συντρέχουν, έστω στο
συντρέχουν, έστω στο  .
.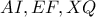 συντρέχουν (στο P).
συντρέχουν (στο P). η τομή των εφαπτομένων του
η τομή των εφαπτομένων του 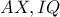 διέρχονται από το
διέρχονται από το 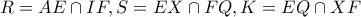 .
. 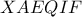 τα
τα 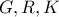 είναι συνευθειακά. Από Pascal για το
είναι συνευθειακά. Από Pascal για το 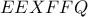 τα
τα 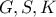 είναι συνευθειακά.
είναι συνευθειακά. 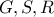 είναι συνευθειακά, άρα τα τρίγωνα
είναι συνευθειακά, άρα τα τρίγωνα 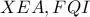 είναι προοπτικά (ως προς άξονα).
είναι προοπτικά (ως προς άξονα).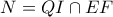 .
.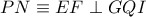 στο τρίγωνο
στο τρίγωνο  τα ύψη
τα ύψη  συντρέχουν. Από θεώρημα Ceva:
συντρέχουν. Από θεώρημα Ceva: 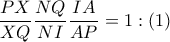
 το μέσο της
το μέσο της 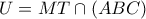 και
και  η προβολή του
η προβολή του  και το
και το  βρίσκεται πάνω στην
βρίσκεται πάνω στην  . Επίσης η
. Επίσης η  διέρχεται από το
διέρχεται από το 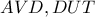 και θεώρημα θαλή με παράλληλες τις
και θεώρημα θαλή με παράλληλες τις 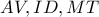 και τέμνουσες τις
και τέμνουσες τις 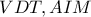 λαμβάνουμε:
λαμβάνουμε: 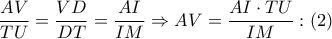
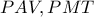 λαμβάνουμε:
λαμβάνουμε: 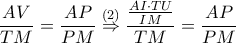 , ή
, ή 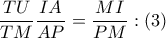
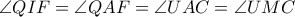 , τα ορθογώνια τρίγωνα
, τα ορθογώνια τρίγωνα 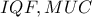 είναι όμοια (με
είναι όμοια (με 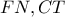 ομόλογα ύψη) και συνεπώς:
ομόλογα ύψη) και συνεπώς: 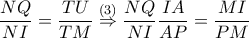 .
.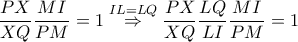 .
. , παίρνουμε
, παίρνουμε  συνευθειακά.
συνευθειακά. .
.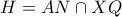 και
και 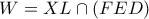 .
.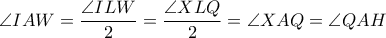 , άρα:
, άρα: 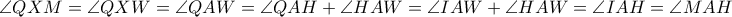 , οπότε το
, οπότε το 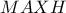 είναι εγγράψιμο.
είναι εγγράψιμο. 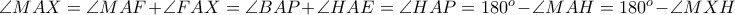 , άρα:
, άρα: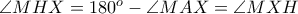 , οπότε
, οπότε 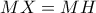 .
.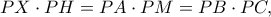 άρα τα
άρα τα 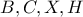 είναι ομοκυκλικά.
είναι ομοκυκλικά.  , το
, το 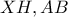 ) είναι το κέντρο του παραπάνω κύκλου.
) είναι το κέντρο του παραπάνω κύκλου.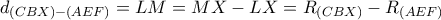 οπότε οι κύκλοι εφάπτονται (εσωτερικά) στο
οπότε οι κύκλοι εφάπτονται (εσωτερικά) στο 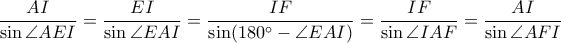 και αφού
και αφού 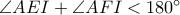 , έχουμε
, έχουμε 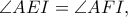 άρα το τετράπλευρο
άρα το τετράπλευρο  είναι εγγράψιμο. Έστω
είναι εγγράψιμο. Έστω 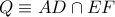 . Το τετράπλευρο
. Το τετράπλευρο 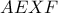 είναι αρμονικό, άρα
είναι αρμονικό, άρα 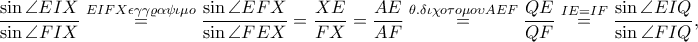 άρα τα σημεία
άρα τα σημεία  είναι συνευθειακά. Θεωρούμε το μέσο
είναι συνευθειακά. Θεωρούμε το μέσο  του
του  και ως γνωστό, η ευθεία
και ως γνωστό, η ευθεία  διέρχεται από το αντιδιαμετρικό
διέρχεται από το αντιδιαμετρικό 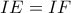 ).
). 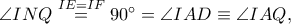 άρα το τετράπλευρο
άρα το τετράπλευρο 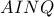 είναι εγγράψιμο. Επιπλέον
είναι εγγράψιμο. Επιπλέον 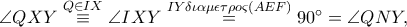 άρα το τετράπλευρο
άρα το τετράπλευρο 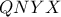 είναι εγγράψιμο. Οι ευθείες
είναι εγγράψιμο. Οι ευθείες 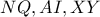 συντρέχουν στο ριζικό κέντρο των κύκλων
συντρέχουν στο ριζικό κέντρο των κύκλων 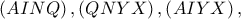 έστω
έστω 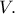 Η
Η 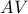 εξωτερική, άρα η δέσμη
εξωτερική, άρα η δέσμη  είναι αρμονική, επομένως το
είναι αρμονική, επομένως το  άρα τα σημεία
άρα τα σημεία 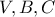 είναι συνευθειακά. Αφού
είναι συνευθειακά. Αφού 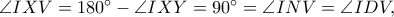 τα σημεία
τα σημεία 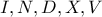 είναι ομοκυκλικά, άρα
είναι ομοκυκλικά, άρα 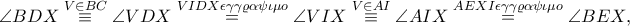 άρα το τετράπλευρο
άρα το τετράπλευρο 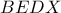 είναι εγγράψιμο και συνεπώς το
είναι εγγράψιμο και συνεπώς το 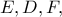 άρα το τετράπλευρο
άρα το τετράπλευρο 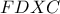 είναι εγγράψιμο. Επομένως
είναι εγγράψιμο. Επομένως 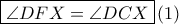 και
και 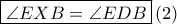 και αφού το
και αφού το 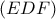 και
και 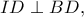 η
η  εφάπτεται του περιγεγραμμένου κύκλου του τριγώνου
εφάπτεται του περιγεγραμμένου κύκλου του τριγώνου 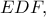 άρα
άρα 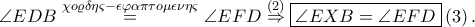 Φέρνουμε την εφαπτομένη στο
Φέρνουμε την εφαπτομένη στο  άρα
άρα 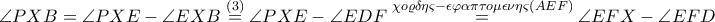
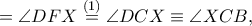 άρα η ευθεία
άρα η ευθεία  εφάπτεται του περιγεγραμμένου κύκλου του τριγώνου
εφάπτεται του περιγεγραμμένου κύκλου του τριγώνου 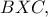 συνεπώς οι περιγεγραμμένοι κύκλοι των τριγώνων
συνεπώς οι περιγεγραμμένοι κύκλοι των τριγώνων 
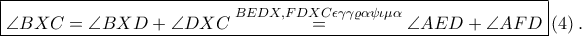 Επιπλέον, το
Επιπλέον, το 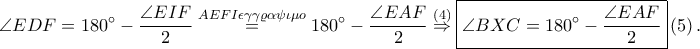 Θεωρούμε το μέσο
Θεωρούμε το μέσο  άρα
άρα 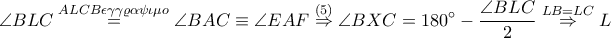 είναι το περίκεντρο του τριγώνου
είναι το περίκεντρο του τριγώνου  και το περίκεντρο του τριγώνου
και το περίκεντρο του τριγώνου