 . Το σημείο
. Το σημείο  είναι τέτοιο, ώστε
είναι τέτοιο, ώστε 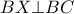 και
και 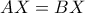 , και το σημείο
, και το σημείο 
τέτοιο, ώστε
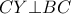 και
και 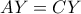 . Οι ευθείες
. Οι ευθείες  και
και  τέμνονται στο σημείο
τέμνονται στο σημείο  .
.Να αποδείξετε ότι η ευθεία
 εφάπτεται του περιγεγραμμένου κύκλου
εφάπτεται του περιγεγραμμένου κύκλου  του τριγώνου
του τριγώνου  .
.
Συντονιστές: vittasko, silouan, rek2
 . Το σημείο
. Το σημείο  είναι τέτοιο, ώστε
είναι τέτοιο, ώστε 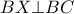 και
και 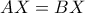 , και το σημείο
, και το σημείο 
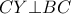 και
και 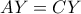 . Οι ευθείες
. Οι ευθείες  και
και  τέμνονται στο σημείο
τέμνονται στο σημείο  .
. εφάπτεται του περιγεγραμμένου κύκλου
εφάπτεται του περιγεγραμμένου κύκλου  του τριγώνου
του τριγώνου  .
.
 και
και 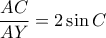 .
.
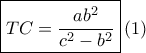
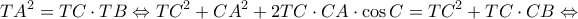
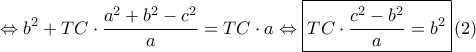
 , η οποία είναι ισοδύναμη με την ισχύουσα
, η οποία είναι ισοδύναμη με την ισχύουσα  και η απόδειξη ολοκληρώθηκε...
και η απόδειξη ολοκληρώθηκε... 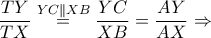 η
η  είναι η εξωτερική διχοτόμος της
είναι η εξωτερική διχοτόμος της 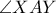 .
.  το κέντρο του
το κέντρο του  .
.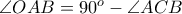 (με
(με  το αντιδιαμετρικό του
το αντιδιαμετρικό του  είναι
είναι 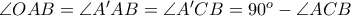 ) και
) και 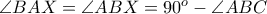 λαμβάνουμε
λαμβάνουμε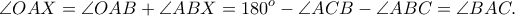
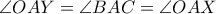 άρα
άρα  η εσωτερική διχοτόμος της
η εσωτερική διχοτόμος της 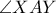 , οπότε
, οπότε  και το ζητούμενο δείχθηκε.
και το ζητούμενο δείχθηκε.Γιώργο, από εκεί που απέδειξες ότιthepigod762 έγραψε: ↑Δευ Οκτ 23, 2023 4:19 pmη
είναι η εξωτερική διχοτόμος της
.
Έστωτο κέντρο του
.
Αφού(με
το αντιδιαμετρικό του
είναι
) και
λαμβάνουμε
Όμοιαάρα
η εσωτερική διχοτόμος της
, οπότε
και το ζητούμενο δείχθηκε.
 εξωτερική διχοτόμος της
εξωτερική διχοτόμος της 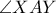 , το ζητούμενο προκύπτει και χωρίς πείραγμα του σχήματος.
, το ζητούμενο προκύπτει και χωρίς πείραγμα του σχήματος. 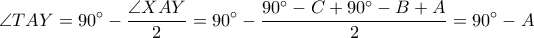
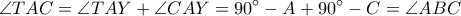
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες