Henri van Aubel έγραψε: ↑Δευ Αύγ 14, 2023 9:29 am
Ευχαριστώ πολύ τον κύριο Κώστα για τη λύση !

Κώστα και λοιποί φίλοι το έχω πει και άλλού, θερμή παράκληση, όταν τουλάχιστον αναφέρεστε σε μένα να χρησιμοποιείτε τον ενικό.
Για την ευγένεια που πρέπει να υπάρχει στις σχέσεις μεταξύ των ανθρώπων, δεν αναφέρεται πουθενά ως προαπαιτούμενο ο πληθυντικός.
Δεν είμαστε δύο ξένοι που συναντιόμαστε για πρώτη φορά στον δρόμο. Έστω και εάν δεν έχει τύχει να βρεθούμε δια ζώσης, γνωριζόμαστε με όρους εκτίμησης αρκετά μεταξύ μας.
Αντί της προσφώνησης "κύριε", είναι προτιμώτερο να με λέτε απλά Κώστα, ακόμα και εάν η διαφορά ηλικίας μας είναι μεγάλη και είναι κάτι που προσδοκώ.
Κώστας Βήττας.
 και
και  το κέντρο του περίκυκλού του. Οι ευθείες
το κέντρο του περίκυκλού του. Οι ευθείες  και
και  τέμνονται στο σημείο
τέμνονται στο σημείο  και έστω
και έστω  το αντιδιαμετρικό του
το αντιδιαμετρικό του  στον περίκυκλο του τριγώνου
στον περίκυκλο του τριγώνου  Να δείξετε ότι οι ευθείες
Να δείξετε ότι οι ευθείες  ,
, και
και  συντρέχουν.
συντρέχουν.
 και ας είναι
και ας είναι  τα μέσα των πλευρών
τα μέσα των πλευρών  αντιστοίχως, και
αντιστοίχως, και  οι προβολές του
οι προβολές του  επί των
επί των  αντιστοίχως.
αντιστοίχως.
 Από τα όμοια ορθογώνια τρίγωνα
Από τα όμοια ορθογώνια τρίγωνα 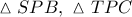 και τα όμοια τρίγωνα
και τα όμοια τρίγωνα 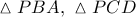 έχουμε:
έχουμε: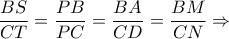

 και
και 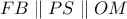 και
και 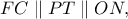 σύμφωνα με το
σύμφωνα με το 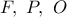 είναι συνευθειακά και το ισοδύναμο ζητούμενο έχει αποδειχθεί.
είναι συνευθειακά και το ισοδύναμο ζητούμενο έχει αποδειχθεί.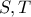 τα σημεία τομής της στο
τα σημεία τομής της στο  με τις ευθείες
με τις ευθείες 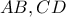 αντίστοιχα και ας είναι
αντίστοιχα και ας είναι 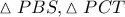
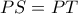 και
και  οπότε στο τρίγωνο
οπότε στο τρίγωνο 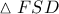 η
η  είναι διχοτόμος και διάμεσος άρα θα είναι και ύψος (ισοσκελές πλέον το τρίγωνο) και συνεπώς
είναι διχοτόμος και διάμεσος άρα θα είναι και ύψος (ισοσκελές πλέον το τρίγωνο) και συνεπώς 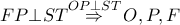 συνευθειακά.
συνευθειακά.  ομοκυκλικά σε κύκλο
ομοκυκλικά σε κύκλο  διαμέτρου
διαμέτρου 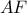 και το ισοδύναμο ζητούμενο έχει αποδειχθεί.
και το ισοδύναμο ζητούμενο έχει αποδειχθεί. και
και  το σημείο Miquel του τετράπλευρου
το σημείο Miquel του τετράπλευρου  συνευθειακα και ότι η ευθεία
συνευθειακα και ότι η ευθεία  είναι καθετή στην
είναι καθετή στην  τότε έχουμε το ζητούμενο.
τότε έχουμε το ζητούμενο.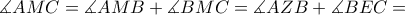
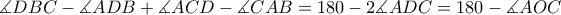 οπότε τα
οπότε τα 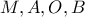 είναι ομοκυκλικα.
είναι ομοκυκλικα.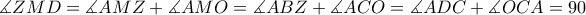
 από το θεώρημα Brocard
από το θεώρημα Brocard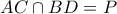 τότε αρκεί να δείξουμε ότι
τότε αρκεί να δείξουμε ότι 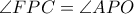 κι αφού
κι αφού 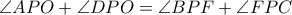 , έπεται πως αρκεί να δείξουμε ότι
, έπεται πως αρκεί να δείξουμε ότι 
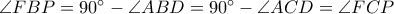 οπότε οι κύκλοι
οπότε οι κύκλοι 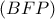 και
και 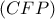 είναι ίσοι και συνεπώς
είναι ίσοι και συνεπώς 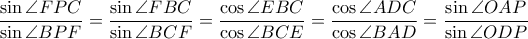
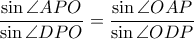 και η απόδειξη ολοκληρώθηκε.
και η απόδειξη ολοκληρώθηκε.