 και ο κύκλος
και ο κύκλος  διαμέτρου
διαμέτρου  Ένα σημείο
Ένα σημείο  κινείται στην πλευρά
κινείται στην πλευρά 
και οι
 επανατέμνουν τον κύκλο στα
επανατέμνουν τον κύκλο στα  αντίστοιχα. Να δείξετε ότι οι
αντίστοιχα. Να δείξετε ότι οι  τέμνονται
τέμνονται σε σημείο
 του
του  και ότι
και ότι 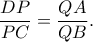
Συντονιστές: vittasko, silouan, rek2
 και ο κύκλος
και ο κύκλος  διαμέτρου
διαμέτρου  Ένα σημείο
Ένα σημείο  κινείται στην πλευρά
κινείται στην πλευρά 
 επανατέμνουν τον κύκλο στα
επανατέμνουν τον κύκλο στα  αντίστοιχα. Να δείξετε ότι οι
αντίστοιχα. Να δείξετε ότι οι  τέμνονται
τέμνονται  του
του  και ότι
και ότι 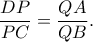
Πολύ καλή κ. Γιώργο!george visvikis έγραψε: ↑Δευ Ιουν 27, 2022 11:28 amΔίνεται τετράγωνοκαι ο κύκλος
διαμέτρου
Ένα σημείο
κινείται στην πλευρά
και οιεπανατέμνουν τον κύκλο στα
αντίστοιχα. Να δείξετε ότι οι
τέμνονται
σε σημείοτου
και ότι
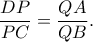
 τέμνονται στο
τέμνονται στο  .
. και
και  είναι εγγράψιμα, έστω στους κύκλους
είναι εγγράψιμα, έστω στους κύκλους 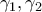 .
. , οπότε είναι
, οπότε είναι συνεπώς το τετράπλευρο
συνεπώς το τετράπλευρο  είναι εγγράψιμο. Όμοια και το τετράπλευρο
είναι εγγράψιμο. Όμοια και το τετράπλευρο  είναι εγγράψιμο
είναι εγγράψιμο 

 τέμνει τον
τέμνει τον  στο
στο  , τότε
, τότε 
 , οπότε το πρώτο ερώτημα αποδείχθηκε.
, οπότε το πρώτο ερώτημα αποδείχθηκε.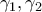 είναι ίσες.
είναι ίσες. η ακτίνα του κύκλου
η ακτίνα του κύκλου  , με
, με  )
)
 , όπως θέλαμε
, όπως θέλαμε 


Ορέστης Λιγνός έγραψε: ↑Δευ Ιουν 27, 2022 2:03 pmΠολύ καλή κ. Γιώργο!george visvikis έγραψε: ↑Δευ Ιουν 27, 2022 11:28 amΑπό Σερβία ο λόγος.png
Δίνεται τετράγωνοκαι ο κύκλος
διαμέτρου
Ένα σημείο
κινείται στην πλευρά
και οιεπανατέμνουν τον κύκλο στα
αντίστοιχα. Να δείξετε ότι οι
τέμνονται
σε σημείοτου
και ότι
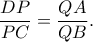
Έστω ότι οι διαγώνιοιτέμνονται στο
.
Ισχυρισμός 1: Τα τετράπλευρακαι
είναι εγγράψιμα, έστω στους κύκλους
.
Απόδειξη: Προφανώς, οπότε είναι
συνεπώς το τετράπλευρο
είναι εγγράψιμο. Όμοια και το τετράπλευρο
είναι εγγράψιμο
Στο πρόβλημα, είναι
άρα αν ητέμνει τον
στο
, τότε
δηλαδή, οπότε το πρώτο ερώτημα αποδείχθηκε.
Για το δεύτερο ερώτημα, χρειαζόμαστε έναν ακόμα Ισχυρισμό:
Ισχυρισμός 2: Οι ακτίνες των κύκλωνείναι ίσες.
Απόδειξη: Είναι, (η ακτίνα του κύκλου
, με
)
οπότε, όπως θέλαμε
Στο πρόβλημα, είναι
άρα
που αποδεικνύει το ζητούμενο.
Έπεσα πάνω στο ωραίο αυτό θέμα και μετά από την πολύ όμορφη λύση του Άριστου Ορέστη, ας δούμε και την διαπραγμάτευση που ακολουθεί και μόνο για λόγους μαθηματικής πολυφωνίας.george visvikis έγραψε: ↑Δευ Ιουν 27, 2022 11:28 amΑπό Σερβία ο λόγος.png
Δίνεται τετράγωνοκαι ο κύκλος
διαμέτρου
Ένα σημείο
κινείται στην πλευρά
και οιεπανατέμνουν τον κύκλο στα
αντίστοιχα. Να δείξετε ότι οι
τέμνονται
σε σημείοτου
και ότι
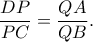
 η άλλη τομή της
η άλλη τομή της  με τον κύκλο εκτός του σημείου
με τον κύκλο εκτός του σημείου  έχουμε:
έχουμε:  Όμως από το εγγράψιμο
Όμως από το εγγράψιμο  προκύπτει
προκύπτει  Από τις
Από τις  έχουμε ότι το σημείο
έχουμε ότι το σημείο  θα είναι σημείο της ευθείας
θα είναι σημείο της ευθείας  δηλαδή
δηλαδή  και έτσι αποδείχτηκε το πρώτο ερώτημα.
και έτσι αποδείχτηκε το πρώτο ερώτημα.  παίρνουμε
παίρνουμε 
 να προκύπτουν όμοια, αφού ισχύει
να προκύπτουν όμοια, αφού ισχύει 
 ή
ή 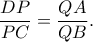
Α)Λίγο διαφορετικά από τον Ορέστηgeorge visvikis έγραψε: ↑Δευ Ιουν 27, 2022 11:28 amΑπό Σερβία ο λόγος.png
Δίνεται τετράγωνοκαι ο κύκλος
διαμέτρου
Ένα σημείο
κινείται στην πλευρά
και οιεπανατέμνουν τον κύκλο στα
αντίστοιχα. Να δείξετε ότι οι
τέμνονται
σε σημείοτου
και ότι
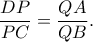
 το κέντρο του τετραγώνου,λόγω των γωνιών
το κέντρο του τετραγώνου,λόγω των γωνιών  τα
τα  είναι εγράψιμμα,συνεπώς
είναι εγράψιμμα,συνεπώς εγγράψιμμο, που αποδεικνύει το ζητούμενο
εγγράψιμμο, που αποδεικνύει το ζητούμενο οπότε και
οπότε και 

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης