Βρείτε όλες τις
 για τις οποίες ισχύει
για τις οποίες ισχύει 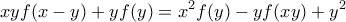
για κάθε
 και
και  (
( )
)Συντονιστές: achilleas, emouroukos, silouan
 για τις οποίες ισχύει
για τις οποίες ισχύει 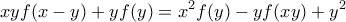
 και
και  (
( )
) τη δοσμένη σχέση για
τη δοσμένη σχέση για 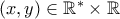 .
. :
: 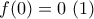
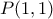 :
: 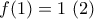
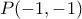 :
: 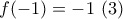
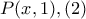 :
: 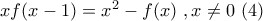
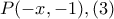 :
: 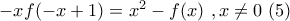
 και απλοποιώντας παίρνουμε:
και απλοποιώντας παίρνουμε: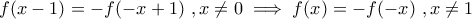 , αλλά και
, αλλά και 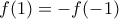 οπότε τελικά:
οπότε τελικά: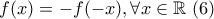 .
.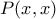 :
: 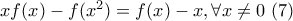
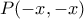 :
: 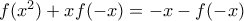 , οπότε κάνοντας χρήση της
, οπότε κάνοντας χρήση της  , έχουμε:
, έχουμε: 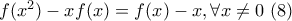 .
. παίρνουμε εύκολα
παίρνουμε εύκολα 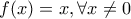 οπότε μαζί με
οπότε μαζί με  έχουμε ότι
έχουμε ότι 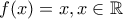 , η οποία εύκολα επαληθεύει την
, η οποία εύκολα επαληθεύει την  και άρα είναι η μοναδική λύση.
και άρα είναι η μοναδική λύση.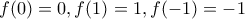 και
και  περιττή
περιττή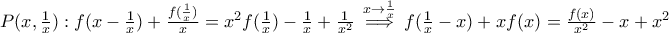
 περιττή,
περιττή, 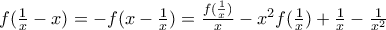
 τελευταίες, έχουμε
τελευταίες, έχουμε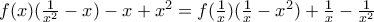
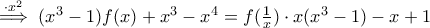
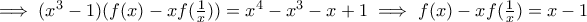
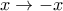 ,
, 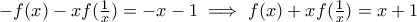
 τελευταίες παίρνουμε
τελευταίες παίρνουμε 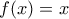 για κάθε
για κάθε  , και σε συνδυασμό με την
, και σε συνδυασμό με την  , είναι
, είναι  για κάθε
για κάθε 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες