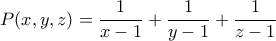 ,
,δεδομένων των συνθηκών
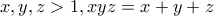 .
.Σχόλιο: Το θέμα ίσως να είναι για το φάκελο της προχωρημένης άλγεβρας Seniors. Έχω μόνο μία λύση (τη λύση κατά την κατασκευή) και δεν μπορώ να κάνω ακριβή εκτίμηση της δυσκολίας. Εικάζω ότι ,δεδομένης της απλότητας των αλγεβρικών εκφράσεων του προβλήματος, θα υπάρχει ευκολότερη λύση.

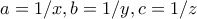 και παίρνουμε
και παίρνουμε  . Αυτό δίνει ότι υπάρχει οξυγώνιο τρίγωνο
. Αυτό δίνει ότι υπάρχει οξυγώνιο τρίγωνο  ώστε
ώστε 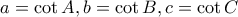 . Τότε
. Τότε 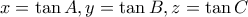 . Επειδή
. Επειδή 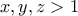 , τότε
, τότε 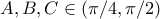 .
.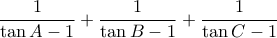
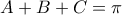 .
.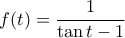 είναι κυρτή στο
είναι κυρτή στο 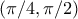 . Πράγματι έχουμε
. Πράγματι έχουμε 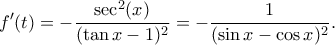
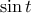 είναι αύξουσα και η
είναι αύξουσα και η 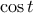 φθίνουσα, άρα η
φθίνουσα, άρα η 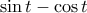 είναι αύξουσα. Είναι επίσης θετική άρα και η
είναι αύξουσα. Είναι επίσης θετική άρα και η 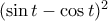 είναι αύξουσα. Το ίδιο θα ισχύει και για την
είναι αύξουσα. Το ίδιο θα ισχύει και για την  .
.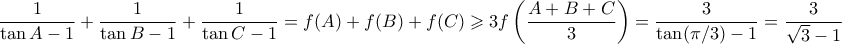
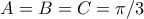 που δίνει
που δίνει 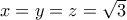
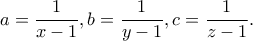 Η
Η 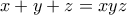 γίνεται
γίνεται 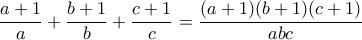
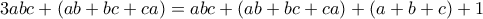 που δίνει
που δίνει 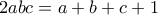 .
.![k = \sqrt[3]{abc} k = \sqrt[3]{abc}](/forum/ext/geomar/texintegr/latexrender/pictures/0396a0ab8bf9ddaa32b311008492e2b8.png) . Από ΑΜ-ΓΜ έχουμε
. Από ΑΜ-ΓΜ έχουμε 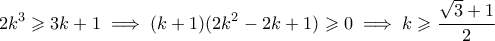
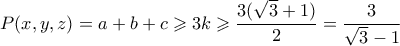
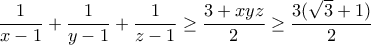 .
.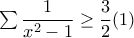 .
.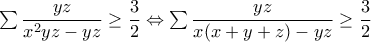 .
.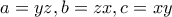 και ισοδύναμα αρκεί:
και ισοδύναμα αρκεί: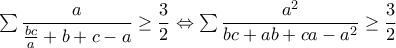 .
.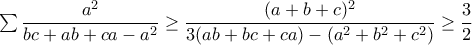 , γιατί η τελευταία ισοδυναμεί με
, γιατί η τελευταία ισοδυναμεί με 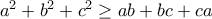 .
.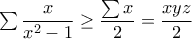 (από την άσκηση του συνδέσμου)
(από την άσκηση του συνδέσμου)![x+y+z\geq 3\sqrt[3]{xyz}\Leftrightarrow xyz\geq 3\sqrt{3} x+y+z\geq 3\sqrt[3]{xyz}\Leftrightarrow xyz\geq 3\sqrt{3}](/forum/ext/geomar/texintegr/latexrender/pictures/e3a6ea335906debd6a80e52f6671f563.png) , από όπου προκύπτει άμεσα η ζητούμενη.
, από όπου προκύπτει άμεσα η ζητούμενη.