 , για την οποία προκύπτει :
, για την οποία προκύπτει :  .
. , για την οποία προκύπτει :
, για την οποία προκύπτει :  .
.Έστω λυμένο το πρόβλημα .
 του
του 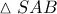 και τον κύκλο ,
και τον κύκλο ,  που έχει κέντρο το
που έχει κέντρο το  και με κάθετη διάμετρο στην
και με κάθετη διάμετρο στην  , την
, την 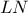 .
.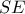 απ αυτή είναι ,
απ αυτή είναι ,  θεωρώ
θεωρώ  .
Το τετράπλευρο
.
Το τετράπλευρο  είναι υπέρ ισοσκελές τραπέζιο με ,
είναι υπέρ ισοσκελές τραπέζιο με ,  και
και  προφανώς δε οι καθεμιά από τις ίσες διαγώνιους του είναι από
προφανώς δε οι καθεμιά από τις ίσες διαγώνιους του είναι από  .
. που έχει δύο πραγματικές ρίζες :
που έχει δύο πραγματικές ρίζες : απορρίπτεται , είτε
απορρίπτεται , είτε  δεκτή κι έτσι
δεκτή κι έτσι 
Στο σχήμα του Θανάση. Από τα τρίγωνα
 έχω
έχω 
 με αντικατάσταση βρίσκω
με αντικατάσταση βρίσκω 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης