KARKAR έγραψε: ↑Δευ Δεκ 11, 2023 1:37 pm
Λόγος επαφών.png
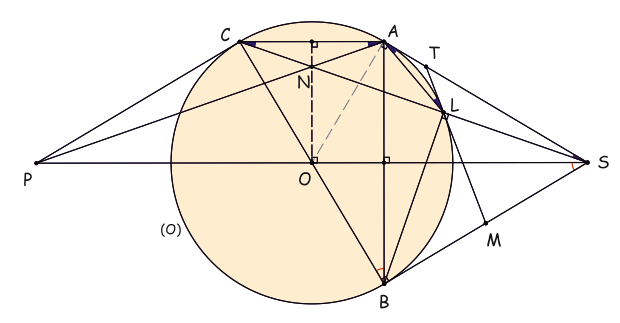
Από σημείο

που κινείται στο εξωτερικό του κύκλου

, σε απόσταση
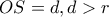
, φέρουμε τα εφαπτόμενα τμήματα
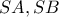
και έστω

το μέσο του

. Η άλλη εφαπτόμενη από το

προς τον κύκλο , τέμνει το

στο σημείο

.
α) Υπολογίστε τον λόγο :
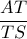
... β) Υπολογίστε το μέγιστο του τμήματος

.
Έστω

το σημείο επαφής της

με τον κύκλο

. Τότε με

(εφαπτομενικά τμήματα στον

)
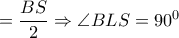
και συνεπώς το δεύτερο (εκτός του

) σημείο

τομής της
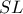
με τον

είναι το αντιδιαμετρικό του
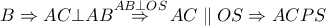
τραπέζιο (όπου

το συμμετρικό του

ως προς το

) και με την μεσοκάθετη στο

της

να είναι και μεσοκάθετη της χορδής (αφού διέρχεται από το κέντρο του κύκλου)
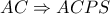
ισοσκελές τραπέζιο , οπότε
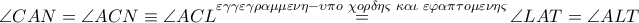
και με
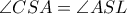
προκύπτει ότι τα τρίγωνα
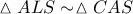
(δύο γωνίες ίσες μια προς μία) με ομόλογα τμήματα τα
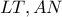
και συνεπώς
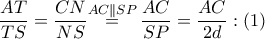
- Λόγος επαφών.png (35.89 KiB) Προβλήθηκε 235 φορές
Από την προφανή ομοιότητα των ορθογωνίων τριγώνων
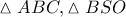
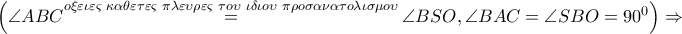
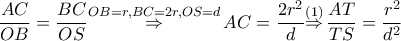
και το πρώτο ζητούμενο έχει αποδειχθεί.
Από
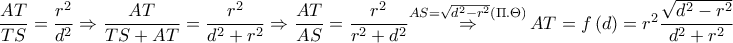
Η συνέχεια (για το ακρότατο της
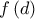
) αφήνεται στον αναγνώστη ή σε κάποιο λογισμικό …

 που κινείται στο εξωτερικό του κύκλου
που κινείται στο εξωτερικό του κύκλου  , σε απόσταση
, σε απόσταση 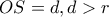 ,
,  και έστω
και έστω  το μέσο του
το μέσο του  . Η άλλη εφαπτόμενη
. Η άλλη εφαπτόμενη  προς τον κύκλο , τέμνει το
προς τον κύκλο , τέμνει το  στο σημείο
στο σημείο  .
.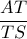 ... β) Υπολογίστε το μέγιστο του τμήματος
... β) Υπολογίστε το μέγιστο του τμήματος  .
.
 το σημείο επαφής της
το σημείο επαφής της  με τον κύκλο
με τον κύκλο  . Τότε με
. Τότε με  (εφαπτομενικά τμήματα στον
(εφαπτομενικά τμήματα στον 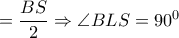 και συνεπώς το δεύτερο (εκτός του
και συνεπώς το δεύτερο (εκτός του  τομής της
τομής της 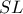 με τον
με τον 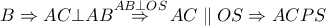 τραπέζιο (όπου
τραπέζιο (όπου  το συμμετρικό του
το συμμετρικό του  ) και με την μεσοκάθετη στο
) και με την μεσοκάθετη στο  να είναι και μεσοκάθετη της χορδής (αφού διέρχεται από το κέντρο του κύκλου)
να είναι και μεσοκάθετη της χορδής (αφού διέρχεται από το κέντρο του κύκλου) 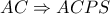 ισοσκελές τραπέζιο , οπότε
ισοσκελές τραπέζιο , οπότε 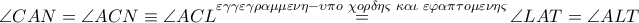 και με
και με 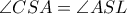 προκύπτει ότι τα τρίγωνα
προκύπτει ότι τα τρίγωνα 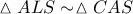 (δύο γωνίες ίσες μια προς μία) με ομόλογα τμήματα τα
(δύο γωνίες ίσες μια προς μία) με ομόλογα τμήματα τα 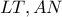 και συνεπώς
και συνεπώς 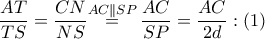
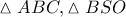
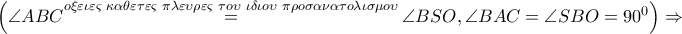
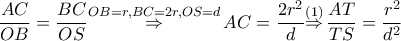 και το πρώτο ζητούμενο έχει αποδειχθεί.
και το πρώτο ζητούμενο έχει αποδειχθεί. 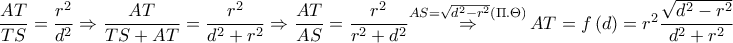 Η συνέχεια (για το ακρότατο της
Η συνέχεια (για το ακρότατο της 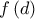 ) αφήνεται στον αναγνώστη ή σε κάποιο λογισμικό …
) αφήνεται στον αναγνώστη ή σε κάποιο λογισμικό … 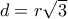 και ισούται με :
και ισούται με : 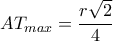 .
.