 τα σημεία
τα σημεία 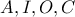 είναι ομοκυκλικά (όπου
είναι ομοκυκλικά (όπου  το έγκεντρο και
το έγκεντρο και  το περίκεντρο).
το περίκεντρο). Ο κύκλος αυτός τέμνει τη
 σε ένα σημείο
σε ένα σημείο  ώστε
ώστε 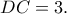 Να βρείτε τις πλευρές του τριγώνου
Να βρείτε τις πλευρές του τριγώνου 
αν γνωρίζετε ότι έχουν μήκη θετικούς ακέραιους αριθμούς.
 τα σημεία
τα σημεία 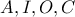 είναι ομοκυκλικά (όπου
είναι ομοκυκλικά (όπου  το έγκεντρο και
το έγκεντρο και  το περίκεντρο).
το περίκεντρο).  σε ένα σημείο
σε ένα σημείο  ώστε
ώστε 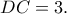 Να βρείτε τις πλευρές του τριγώνου
Να βρείτε τις πλευρές του τριγώνου 
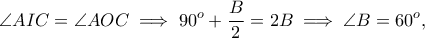
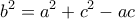 (
( )
) άρα το τρίγωνο
άρα το τρίγωνο  είναι ισόπλευρο. Επομένως
είναι ισόπλευρο. Επομένως 
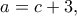 οπότε η (
οπότε η ( ) γίνεται τελικά
) γίνεται τελικά 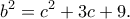
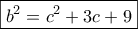
 . Θέλουμε να υπάρχει διπλάσιο γινόμενο (έτσι θέλει η γνωστή ταυτότητα), αλλά και να μη χαλάσουν τα τετράγωνα. Τη δουλειά αυτή την κάνει άψογα το 4. Πολλαπλασιάζουμε λοιπόν τα μέλη επί 4, οπότε λαμβάνουμε
. Θέλουμε να υπάρχει διπλάσιο γινόμενο (έτσι θέλει η γνωστή ταυτότητα), αλλά και να μη χαλάσουν τα τετράγωνα. Τη δουλειά αυτή την κάνει άψογα το 4. Πολλαπλασιάζουμε λοιπόν τα μέλη επί 4, οπότε λαμβάνουμε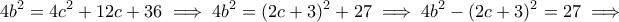
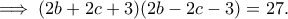
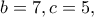 οπότε
οπότε 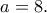
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες