Εξειδικευμένη ισότητα

KARKAR · #1

: Εξειδικευμένη ισότητα.png (14.21 KiB) Προβλήθηκε 813 φορές

Στην διάμετρο

ενός ημικυκλίου βρίσκεται σημείο

, ώστε : $AP=\dfrac{AB}{4}$ . Σημείο

κινείται στο ημικύκλιο . Συνδέω το

με το μέσο

της

. α) Δείξτε ότι : PM=PS

.

β) Αν : AP=2 , PB=6

, βρείτε την θέση του

, για την οποία : PM=PS=5

.

#2

KARKAR έγραψε: ↑
Κυρ Ιούλ 20, 2025 9:47 am
Εξειδικευμένη ισότητα.pngΣτην διάμετρο ενός ημικυκλίου βρίσκεται σημείο , ώστε : $AP=\dfrac{AB}{4}$ . Σημείο

κινείται στο ημικύκλιο . Συνδέω το με το μέσο της . α) Δείξτε ότι : .

β) Αν : , βρείτε την θέση του , για την οποία : .

.

: exidik.png (20.25 KiB) Προβλήθηκε 806 φορές

.
Φέρνουμε $PT\perp SB$ , οπότε είναι PT//AS

. Άρα, αφού $AP=\dfrac{AB}{4}$ , έπεται $ST=\dfrac{SB}{4}$ . 'Ομως $SM=\dfrac{SB}{2}$ , οπότε $TM=\dfrac{SB}{4}=ST$ . Με άλλα λόγια, η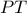

είναι μεσοκάθετος του

, οπότε

, όπως θέλαμε.

β) $25=PS^ 2= SQ^2+PQ^2= AQ\cdot QB+ PQ^2= (2+x)(6-x)+x^2$ . Άρα (πρωτοβάθμια) $x=\dfrac {13}{4}$ .

#3

KARKAR έγραψε: ↑
Κυρ Ιούλ 20, 2025 9:47 am
Στην διάμετρο ενός ημικυκλίου βρίσκεται σημείο , ώστε : $AP=\dfrac{AB}{4}$ . Σημείο

κινείται στο ημικύκλιο . Συνδέω το με το μέσο της . α) Δείξτε ότι : .

β) Αν : , βρείτε την θέση του , για την οποία : .

.

: exidik 2.png (22.08 KiB) Προβλήθηκε 784 φορές

.
Ας το δούμε και με Αναλυτική Γεωμετρία επειδή είναι άμεσο, χωρίς σκέψη. Νομίζω ότι είναι ιδιαίτερα κατάλληλη άσκηση Αναλυτικής Γεωμετρίας για τους μαθητές μας, ιδίως όταν βρίσκονται στην διαδικασία μάθησης του κλάδου.

Με αρχή των αξόνων το μέσο

της διαμέτρου ημικυκλίου ακτίνας

έχουμε $A(-R,0),\, B(R,0), P\left ( -\dfrac {R}{2}, \,0 \right), \,S(a,b)$ όπου a^2+b^2=R^2

. Έπεται ότι $M\left ( \dfrac {a+R}{2}, \,\dfrac {b}{2}, \,\right)$ . Άρα

$PS^2= \left ( a+\dfrac {R}{2} \right)^2 +b^2= (a^2+b^2)+ aR+\dfrac {R^2}{4} = R^2+ aR+\dfrac {R^2}{4}= \dfrac {5R^2}{4} + aR$ και

$PM^2= \left ( \dfrac {a+R}{2}+\dfrac {R}{2} \right)^2 +\dfrac {b^2}{4}= \left ( \dfrac {a}{2}+R \right)^2 +\dfrac {b^2}{4} =$

$=\dfrac {a^2+b^2}{4}+ aR+R^2= \dfrac {R^2}{4}+ aR+R^2= \dfrac {5R^2}{4}+ aR$ , ίδιο με πριν.

Άρα PM=PS

.

(Αν θέλουμε απάντηση και στο β), όπου R=4

, είναι άμεσο από το $25=PS^2 =\dfrac {5R^2}{4} + aR$ )

Μιχάλης Τσουρακάκης · #4

KARKAR έγραψε: ↑
Κυρ Ιούλ 20, 2025 9:47 am
Εξειδικευμένη ισότητα.pngΣτην διάμετρο ενός ημικυκλίου βρίσκεται σημείο , ώστε : $AP=\dfrac{AB}{4}$ . Σημείο

κινείται στο ημικύκλιο . Συνδέω το με το μέσο της . α) Δείξτε ότι : .

β) Αν : , βρείτε την θέση του , για την οποία : .

A)Με

συμμετρικό του

ως προς

κι επειδή προφανώς BO=2OP=OA

(

είναι κ.βάρους του τριγώνου CSB

)

το

είναι το κέντρο του ημικυκλίου ,άρα $COM \bot SB$ οπότε SP=PC=PM

B)Θεωρώντας τον κύκλο (P,PS=5)

θα είναι

και

$\dfrac{BS^2}{2} =BD.BE=11 \Rightarrow BS= \sqrt{22}$

Ο κύκλος $(B, \sqrt{22} )$ τέμνει το ημικύκλιο στο ζητούμενο σημείο

: Εξειδικευμένη ισότητα.png (38.2 KiB) Προβλήθηκε 775 φορές

#5

KARKAR έγραψε: ↑
Κυρ Ιούλ 20, 2025 9:47 am
Στην διάμετρο ενός ημικυκλίου βρίσκεται σημείο , ώστε : $AP=\dfrac{AB}{4}$ . Σημείο

κινείται στο ημικύκλιο . Συνδέω το με το μέσο της . α) Δείξτε ότι : .

β) Αν : , βρείτε την θέση του , για την οποία : .

.

Οι $SP, \, PM$ είναι διάμεσοι των τριγώνων ASO, SPB

αντίστοιχα. Από το θεώρημα των διαμέσων σε καθένα από αυτά τα τρίγωνα έχουμε

$2SP^2+2\left (\dfrac {R}{2} \right )^2= AS^2+R^2,\, {\color {red} (*)}$ και

$SP^2+\left (\dfrac {3R}{2} \right )^2= 2PM ^2 +\dfrac {SB^2}{2}$ , ισοδύναμα

$2SP^2+\dfrac {9R^2}{2} \righτ = 4PM ^2 +SB^2 ,\, {\color {red} (**)}$

Προσθέτοντας κατά μέλη τις ${\color {red} (*), (**)}$ και με χρήση του AS^2+ SB^2=AB^2=4R^2

παίρνουμε

, ισοδύναμα

4SP^2=4PM^2

, από όπου το ζητούμενο.

#6

KARKAR έγραψε: ↑
Κυρ Ιούλ 20, 2025 9:47 am
Εξειδικευμένη ισότητα.pngΣτην διάμετρο ενός ημικυκλίου βρίσκεται σημείο , ώστε : $AP=\dfrac{AB}{4}$ . Σημείο

κινείται στο ημικύκλιο . Συνδέω το με το μέσο της . α) Δείξτε ότι : .

β) Αν : , βρείτε την θέση του , για την οποία : .

: Εξειδικευμένη ισότητα_a.png (21.47 KiB) Προβλήθηκε 731 φορές

α)Ας είναι

το κέντρο του δεδομένου ημικυκλίου , γράφω μέσα σ αυτό το ημικύκλιο διαμέτρου ,

.

Η

τέμνει το μικρό ημικύκλιο στο

. Το τετράπλευρο STOM

είναι ορθογώνιο κι επειδή ,

$PT = PO\,\,,\,\,ST = OM\,\,\,\kappa \alpha \iota \,\,\widehat {{\alpha _1}} + 90^\circ = \widehat {{\alpha _2}} + 90^\circ$ , $\boxed{\vartriangle PTS = \vartriangle POM \Rightarrow PS = PM}$

β) Το

είναι η τομή του κύκλου $\left( {P,5} \right)$ με το δεδομένο ημικύκλιο .

: Εξειδικευμένη ισότητα_b.png (24.69 KiB) Προβλήθηκε 731 φορές

Για τους υπολογισμούς: Από το σχήμα , AD = OH = 3

. Αν

η προβολή του

στην

, θέτω $OT = x \Rightarrow TH = 3 - x$ κι έχω :

$\displaystyle \left\{ \begin{gathered} O{S^2} = O{T^2} + S{T^2} \hfill \\ S{T^2} = TH \cdot TD \hfill \\ \end{gathered} \right. \Rightarrow \left\{ \begin{gathered} 16 = {x^2} + {h^2} \hfill \\ {h^2} = \left( {3 - x} \right)\left( {7 + x} \right) \hfill \\ \end{gathered} \right.$ .

Διώχνω το

και προκύπτει , $16 = {x^2} + \left( {3 - x} \right)\left( {7 + x} \right) \Leftrightarrow 4x = 5 \Leftrightarrow \boxed{x = \frac{5}{4}}$ .

#7

KARKAR έγραψε: ↑
Κυρ Ιούλ 20, 2025 9:47 am
Στην διάμετρο ενός ημικυκλίου βρίσκεται σημείο , ώστε : $AP=\dfrac{AB}{4}$ . Σημείο

κινείται στο ημικύκλιο . Συνδέω το με το μέσο της . α) Δείξτε ότι : .

β) Αν : , βρείτε την θέση του , για την οποία : .

: exidik 4.png (28.86 KiB) Προβλήθηκε 712 φορές

.
Ισχύει $\cos B= \dfrac {SB}{AB}= \dfrac {2b}{4a}=\dfrac {b}{2a}$ . Τώρα, από τον Νόμο των συνημιτόνων στο τρίγωνο PSB

έχουμε

$PS^2= (3a)^2+(2b)^2-2\cdot 3a \cdot 2b \cos B= 9a^2+4b^2- 12ab \cdot \dfrac {b}{2a} =9a^2-2b^2$ .

Επίσης, από τον Νόμο των συνημιτόνων στο τρίγωνο PMB

έχουμε

$PM^2= (3a)^2+b^2-2\cdot 3a \cdot b \cos B= 9a^2+b^2- 6ab \cdot \dfrac {b}{2a} =9a^2-2b^2$ (το ίδιο με πριν). 'Αρα PS=PM

Μιχάλης Τσουρακάκης · #8

KARKAR έγραψε: ↑
Κυρ Ιούλ 20, 2025 9:47 am
Εξειδικευμένη ισότητα.pngΣτην διάμετρο ενός ημικυκλίου βρίσκεται σημείο , ώστε : $AP=\dfrac{AB}{4}$ . Σημείο

κινείται στο ημικύκλιο . Συνδέω το με το μέσο της . α) Δείξτε ότι : .

β) Αν : , βρείτε την θέση του , για την οποία : .

Αλλιώς για το πρώτο ερώτημα

Με

μέσον του

η

είναι διάμεσος του τραπεζίου SMOA

.

Άρα

μεσοκάθετος της

οπότε

: ...ισότητα.png (24.73 KiB) Προβλήθηκε 679 φορές

Εξειδικευμένη ισότητα

Εξειδικευμένη ισότητα

Re: Εξειδικευμένη ισότητα

Re: Εξειδικευμένη ισότητα

Re: Εξειδικευμένη ισότητα

Re: Εξειδικευμένη ισότητα

Re: Εξειδικευμένη ισότητα

Re: Εξειδικευμένη ισότητα

Re: Εξειδικευμένη ισότητα

Μέλη σε σύνδεση