Η διαίρεση
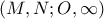
είναι αρμονική, όπου

το σημείο στο άπειρο της ευθείας

. Αν η παράλληλη από
το

της

τέμνει τον κύκλο

στο σημείο

, τότε η δέσμη
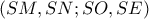
είναι αρμονική, οπότε οι τομές
των ακτίνων αυτής της δέσμης με τον κύκλο

ορίζουν το αρμονικό τετράπλευρο

.
Ως εκ τούτου, η διαγώνιος

του αρμονικού τετραπλεύρου διέρχεται από το σημείο τομής

των εφαπτομένων
του κύκλου

στα σημεία

,

(ιδιότητα αρμονικού τετραπλεύρου).
Είναι
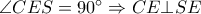
, και εφόσον
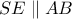
, τότε
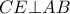
. Έστω
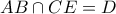
. Τότε

.
Τα σημεία

,

είναι συμμετρικά ως προς την διάμετρο

, δηλαδή η

μεσοκάθετος της

, και ως εκ τούτου
διέρχεται από το

.
Στο ορθογώνιο τρίγωνο
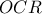
ισχύει
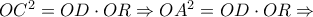
η διαίρεση
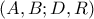
είναι αρμονική

.
Επίσης, στο ορθογώνιο τρίγωνο

οι σεβιανές

και
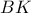
τέμνονται στο σημείο

.
Αν
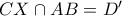
, και εφόσον η ευθεία
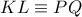
διέρχεται από το σημείο

της

, από γνωστό λήμμα (*) έχουμε
ότι η διαίρεση
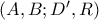
είναι αρμονική

.
Από

και

προκύπτει ότι

, από το οποίο έχουμε ότι
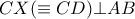
.
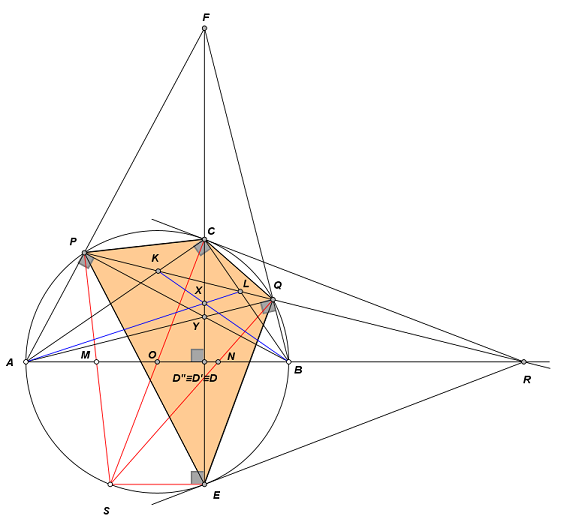
- perp_from_intersec4.png (61.21 KiB) Προβλήθηκε 920 φορές
Απομένει να αποδείξουμε ότι

.
Έστω
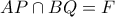
. Τότε στο τρίγωνο
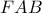
το

είναι προφανώς το ορθόκεντρο, οπότε
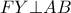
.
Έστω
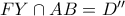
. Προκύπτει ότι η διαίρεση
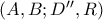
είναι αρμονική (λήμμα

), και εφόσον η διαίρεση
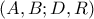
είναι αρμονική, τότε

, δηλαδή,
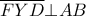
, που σημαίνει ότι και

.
(*) Λήμμα : Σε τρίγωνο

, θεωρούμε τρία σημεία

,

,

στο εσωτερικό των πλευρών

,

και

, αντίστοιχα.
Αν

το σημείο τομής της ευθείας

με την ευθεία

(υποθέτουμε ότι το

βρίσκεται μεταξύ των

και

),
τότε η διαίρεση
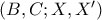
είναι αρμονική, αν και μόνο αν, οι σεβιανές

,

,
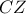
είναι συντρέχουσες.
 κύκλου
κύκλου  κέντρου
κέντρου  θεωρούμε τα σημεία
θεωρούμε τα σημεία  εκατέρωθεν του
εκατέρωθεν του  με
με 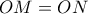 και ας είναι
και ας είναι  πλησιέστερο στο
πλησιέστερο στο  .
. 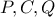 είναι τα σημεία τομής των
είναι τα σημεία τομής των 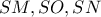 με τον κύκλο αντίστοιχα, με
με τον κύκλο αντίστοιχα, με  διάφορο των
διάφορο των 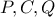 και
και  τα σημεία τομής της
τα σημεία τομής της  με τις
με τις  αντίστοιχα , να δειχτεί ότι
αντίστοιχα , να δειχτεί ότι  , όπου
, όπου 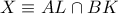 και
και 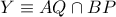

 .
.
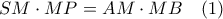 και
και 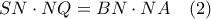 .
. και
και  .
.  και
και  είναι ίσα, οπότε
είναι ίσα, οπότε  .
.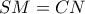 ,
,  και
και 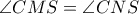 (
(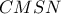 παραλληλόγραμμο), οπότε η
παραλληλόγραμμο), οπότε η  γίνεται
γίνεται 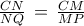 ,
, και
και 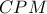 , που με τη σειρά της δίνει τη γωνιακή ισότητα
, που με τη σειρά της δίνει τη γωνιακή ισότητα 
 έχουμε ότι
έχουμε ότι 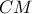 ,
,  ισογώνιες ως προς τις πλευρές της γωνίας
ισογώνιες ως προς τις πλευρές της γωνίας 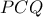 .
. , και ας είναι
, και ας είναι 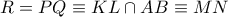 . Από το γνωστό θεώρημα των ισογώνιων
. Από το γνωστό θεώρημα των ισογώνιων  και
και  είναι ισογώνιες ως προς τις πλευρές της γωνίας
είναι ισογώνιες ως προς τις πλευρές της γωνίας 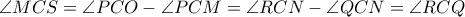 (β). Αλλά,
(β). Αλλά, 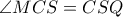
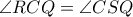 , δηλαδή, η
, δηλαδή, η  εφαπτομένη του κύκλου
εφαπτομένη του κύκλου  στο
στο  .
.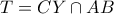 , τότε από γνωστό λήμμα η διαίρεση
, τότε από γνωστό λήμμα η διαίρεση 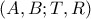 είναι αρμονική
είναι αρμονική 
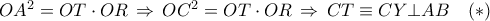 .
.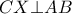 .
.
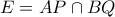 , τότε το
, τότε το  είναι το ορθόκεντρο του τριγώνου
είναι το ορθόκεντρο του τριγώνου  , οπότε
, οπότε  . Έστω
. Έστω  .
. 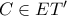 . Από γνωστό λήμμα η διαίρεση
. Από γνωστό λήμμα η διαίρεση 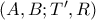 είναι αρμονική
είναι αρμονική  , εφόσον
, εφόσον 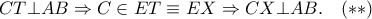
 ,
,  προκύπτει το αποδεικτέο.
προκύπτει το αποδεικτέο. και
και 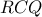 .
. Αποδεικνύεται ότι για κάθε σημείο
Αποδεικνύεται ότι για κάθε σημείο  του ύψους
του ύψους  του ορθογωνίου τριγώνου
του ορθογωνίου τριγώνου 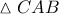 της εκφώνησης, προκύπτει ότι το σημείο
της εκφώνησης, προκύπτει ότι το σημείο 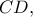 όπου
όπου 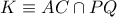 και
και 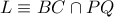 και
και 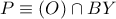 και
και 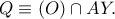
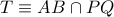 έχουμε ότι η σημειοσειρά
έχουμε ότι η σημειοσειρά  είναι αρμονική.
είναι αρμονική.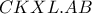 έχουμε ότι η δέσμη
έχουμε ότι η δέσμη 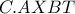 είναι αρμονική και άρα, η ακτίνα της
είναι αρμονική και άρα, η ακτίνα της  περνάει από το σημείο
περνάει από το σημείο 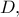 ως το αρμονικό συζυγές του
ως το αρμονικό συζυγές του  ως προς τα σημεία
ως προς τα σημεία  και προκύπτει έτσι, ότι οι ευθείες
και προκύπτει έτσι, ότι οι ευθείες 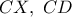 ταυτίζονται.
ταυτίζονται.
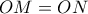 όπου
όπου 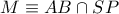 και
και 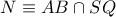 με το σημείο
με το σημείο 
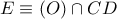 και έχουμε ότι το τετράπλευρο
και έχουμε ότι το τετράπλευρο  είναι αρμονικό και επομένως, η δέσμη
είναι αρμονικό και επομένως, η δέσμη 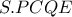 είναι αρμονική.
είναι αρμονική.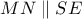 και συμπεραίνεται έτσι ότι
και συμπεραίνεται έτσι ότι  συντρέχουν στο
συντρέχουν στο  είναι το συζυγές αρμονικό του
είναι το συζυγές αρμονικό του  , συμπεράνουμε ότι η ευθεία
, συμπεράνουμε ότι η ευθεία 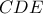 είναι η πολική του
είναι η πολική του 
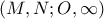 είναι αρμονική, όπου
είναι αρμονική, όπου  το σημείο στο άπειρο της ευθείας
το σημείο στο άπειρο της ευθείας  , τότε η δέσμη
, τότε η δέσμη 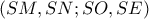 είναι αρμονική, οπότε οι τομές
είναι αρμονική, οπότε οι τομές  των εφαπτομένων
των εφαπτομένων 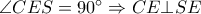 , και εφόσον
, και εφόσον 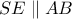 , τότε
, τότε 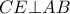 . Έστω
. Έστω 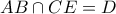 . Τότε
. Τότε  .
. , και ως εκ τούτου
, και ως εκ τούτου 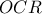 ισχύει
ισχύει 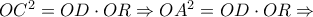 η διαίρεση
η διαίρεση 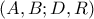 είναι αρμονική
είναι αρμονική  οι σεβιανές
οι σεβιανές  και
και 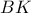 τέμνονται στο σημείο
τέμνονται στο σημείο 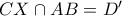 , και εφόσον η ευθεία
, και εφόσον η ευθεία 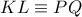 διέρχεται από το σημείο
διέρχεται από το σημείο 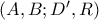 είναι αρμονική
είναι αρμονική  , από το οποίο έχουμε ότι
, από το οποίο έχουμε ότι 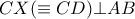 .
.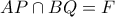 . Τότε στο τρίγωνο
. Τότε στο τρίγωνο 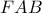 το
το 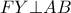 .
.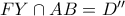 . Προκύπτει ότι η διαίρεση
. Προκύπτει ότι η διαίρεση 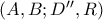 είναι αρμονική (λήμμα
είναι αρμονική (λήμμα  , δηλαδή,
, δηλαδή, 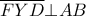 , που σημαίνει ότι και
, που σημαίνει ότι και  , θεωρούμε τρία σημεία
, θεωρούμε τρία σημεία  στο εσωτερικό των πλευρών
στο εσωτερικό των πλευρών  ,
,  και
και  το σημείο τομής της ευθείας
το σημείο τομής της ευθείας  με την ευθεία
με την ευθεία  και
και 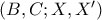 είναι αρμονική, αν και μόνο αν, οι σεβιανές
είναι αρμονική, αν και μόνο αν, οι σεβιανές  ,
,  ,
, 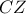 είναι συντρέχουσες.
είναι συντρέχουσες. Από το μη κυρτό εγγεγραμμένο στον κύκλο
Από το μη κυρτό εγγεγραμμένο στον κύκλο 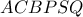 σύμφωνα με το
σύμφωνα με το 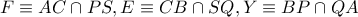 είναι συνευθειακά.
είναι συνευθειακά.  να διχοτομούνται προκύπτει ότι το
να διχοτομούνται προκύπτει ότι το 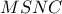 είναι παραλληλόγραμμο οπότε :
είναι παραλληλόγραμμο οπότε : 

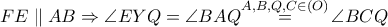
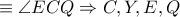 ομοκυκλικά και με
ομοκυκλικά και με 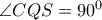 (
(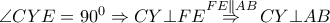
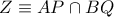 τότε από τη διάμετρο
τότε από τη διάμετρο  είναι τα δύο ύψη του τριγώνου
είναι τα δύο ύψη του τριγώνου 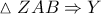 το ορθόκεντρο του τριγώνου και συνεπώς
το ορθόκεντρο του τριγώνου και συνεπώς 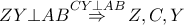 συνευθειακά
συνευθειακά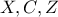 είναι συνευθειακά.
είναι συνευθειακά.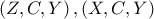 με δύο κοινά σημεία (τα
με δύο κοινά σημεία (τα 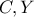 ) προκύπτει ότι τα
) προκύπτει ότι τα 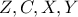 είναι συνευθειακά και με
είναι συνευθειακά και με 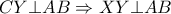 και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. 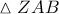 και τυχούσα ευθεία
και τυχούσα ευθεία  που διέρχεται από το
που διέρχεται από το  είναι σημεία της
είναι σημεία της 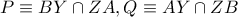 να δείξετε ότι το σημείο
να δείξετε ότι το σημείο 
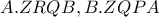 έχουν κοινή ακτίνα την
έχουν κοινή ακτίνα την 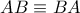 και οι ομόλογες ακτίνες τους τέμνονται σε σημεία συνευθειακά
και οι ομόλογες ακτίνες τους τέμνονται σε σημεία συνευθειακά 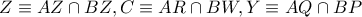 και συνεπώς έχουν ίσους διπλούς λόγους . Οι ακτίνες αυτές των δεσμών τέμνουν τις
και συνεπώς έχουν ίσους διπλούς λόγους . Οι ακτίνες αυτές των δεσμών τέμνουν τις  στα σημεία
στα σημεία 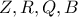 και
και 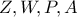 και συνεπώς θα είναι και
και συνεπώς θα είναι και 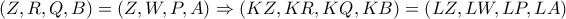 και επειδή οι δέσμες αυτές έχουν μία κοινή ακτίνα την
και επειδή οι δέσμες αυτές έχουν μία κοινή ακτίνα την 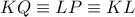 τα σημεία τομής των ομολόγων άλλων τριών ακτινών τους θα είναι συνευθειακά, δηλαδή τα
τα σημεία τομής των ομολόγων άλλων τριών ακτινών τους θα είναι συνευθειακά, δηλαδή τα 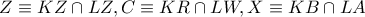 θα είναι συνευθειακά, δηλαδή
θα είναι συνευθειακά, δηλαδή 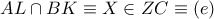 και το Λήμμα έχει αποδειχτεί.
και το Λήμμα έχει αποδειχτεί.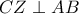 με
με 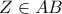 . Είναι
. Είναι 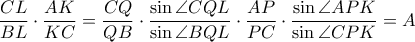 .
. 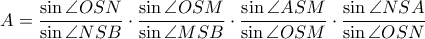 .
. 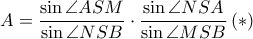
 και
και 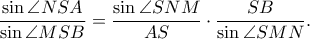
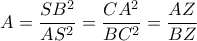 .
. 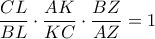 οπότε από αντίστροφο Θ. Ceva οι
οπότε από αντίστροφο Θ. Ceva οι 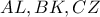 συντρέχουν οπότε
συντρέχουν οπότε 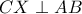 .
. .
.  .
.  .
.  .
. 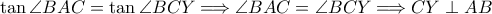 .
.  οπότε
οπότε 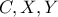 συνευθειακά κι έτσι
συνευθειακά κι έτσι  .
.