Στην υποτείνουσα
 , ορθογωνίου τριγώνου
, ορθογωνίου τριγώνου  , ολισθαίνει τμήμα
, ολισθαίνει τμήμα  .
.Φέρω τα τμήματα :
 και
και  . Εξετάστε αν αληθεύει ο ισχυρισμός ,
. Εξετάστε αν αληθεύει ο ισχυρισμός , ότι το εμβαδόν του τριγώνου
 , μεγιστοποιείται όταν
, μεγιστοποιείται όταν  .
.Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 , ορθογωνίου τριγώνου
, ορθογωνίου τριγώνου  , ολισθαίνει τμήμα
, ολισθαίνει τμήμα  .
. και
και  . Εξετάστε αν αληθεύει ο ισχυρισμός ,
. Εξετάστε αν αληθεύει ο ισχυρισμός ,  , μεγιστοποιείται όταν
, μεγιστοποιείται όταν  .
.Το τρίγωνο
 είναι σταθερό με εμβαδόν έστω
είναι σταθερό με εμβαδόν έστω  και
και  σταθερό .
σταθερό . οι προβολές των
οι προβολές των  στις
στις  . Τα τρίγωνα
. Τα τρίγωνα  είναι όμοια με το τρίγωνο
είναι όμοια με το τρίγωνο  .
. όπου
όπου  το σημείο διασταύρωσης των
το σημείο διασταύρωσης των  . Έτσι:
. Έτσι:  .
.  σταθερό και άρα το εμβαδόν
σταθερό και άρα το εμβαδόν  γίνεται μέγιστο όταν:
γίνεται μέγιστο όταν: 
 απέχουν εξ ίσου από τα άκρα
απέχουν εξ ίσου από τα άκρα  συνεπώς
συνεπώς  .
. ( αφού
( αφού  ) και άρα
) και άρα  .
.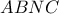 είναι σταθερό, και το
είναι σταθερό, και το  σταθερό
σταθερό 
 είναι σταθερό, το γινόμενο μεγιστοποιείται όταν
είναι σταθερό, το γινόμενο μεγιστοποιείται όταν  .
. (μία πλευρά και παρά την βάση γωνίες ίσες), άρα
(μία πλευρά και παρά την βάση γωνίες ίσες), άρα 
 θα είναι ίσο με αυτά,
θα είναι ίσο με αυτά,  σαν εμβαδόν και σαν σημείο να μην δημιουργεί σύγχυση)
σαν εμβαδόν και σαν σημείο να μην δημιουργεί σύγχυση)Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 26 επισκέπτες