 είναι ισοσκελές και τα
είναι ισοσκελές και τα  μέσα των ίσων πλευρών του .
μέσα των ίσων πλευρών του .Στην
 θεωρώ τυχόν σημείο
θεωρώ τυχόν σημείο  . Εντοπίστε - κατά προτίμηση κατασκευαστικά -
. Εντοπίστε - κατά προτίμηση κατασκευαστικά -σημείο
 της
της  , ώστε το
, ώστε το  να είναι ο γεωμετρικός μέσος των
να είναι ο γεωμετρικός μέσος των 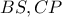 .
.Αν το τρίγωνο είναι ισόπλευρο , δείξτε ότι :
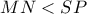 .
.Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 είναι ισοσκελές και τα
είναι ισοσκελές και τα  μέσα των ίσων πλευρών του .
μέσα των ίσων πλευρών του . θεωρώ τυχόν σημείο
θεωρώ τυχόν σημείο  . Εντοπίστε - κατά προτίμηση κατασκευαστικά -
. Εντοπίστε - κατά προτίμηση κατασκευαστικά - της
της  , ώστε το
, ώστε το  να είναι ο γεωμετρικός μέσος των
να είναι ο γεωμετρικός μέσος των 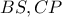 .
.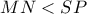 .
.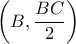 τέμνει την κάθετη από το
τέμνει την κάθετη από το  στην
στην  στο σημείο
στο σημείο  Στη συνέχεια φέρνω την κάθετη από το
Στη συνέχεια φέρνω την κάθετη από το  στην
στην που τέμνει την
που τέμνει την  στο
στο 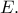 Τέλος, η παράλληλη από το
Τέλος, η παράλληλη από το  στην
στην  τέμνει την
τέμνει την  στο ζητούμενο σημείο
στο ζητούμενο σημείο 

Για την περίπτωση του ισοπλεύρου. Έστω
 η πλευρά του ισοπλεύρου και
η πλευρά του ισοπλεύρου και 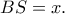 Τότε θα είναι
Τότε θα είναι 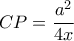 και με νόμο συνημιτόνων στο
και με νόμο συνημιτόνων στο 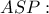
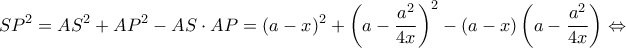

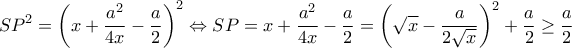
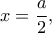 δηλαδή όταν το
δηλαδή όταν το  ταυτιστεί με το
ταυτιστεί με το  Σε κάθε άλλη θέση είναι
Σε κάθε άλλη θέση είναι 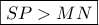
 το μέσο της βάσης
το μέσο της βάσης  , τότε :
, τότε : 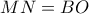 . Γράφω τον κύκλο κέντρου
. Γράφω τον κύκλο κέντρου  ,
,  . Η εφαπτομένη σ' αυτόν από το
. Η εφαπτομένη σ' αυτόν από το  ,
, , αφού είναι απλό να δείξουμε ότι :
, αφού είναι απλό να δείξουμε ότι : 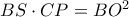 .
. , καθώς το
, καθώς το 
 (σημείο επαφής ) και
(σημείο επαφής ) και  . Ας επισημανθεί
. Ας επισημανθεί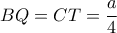 και
και 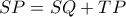 κ.λ.π. Σε κάθε περίπτωση
κ.λ.π. Σε κάθε περίπτωσηΜέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες