Όροι γεωμετρικής προόδου
Συντονιστές: achilleas, emouroukos, silouan
-
orestisgotsis
- Δημοσιεύσεις: 1753
- Εγγραφή: Σάβ Φεβ 25, 2012 10:19 pm
Όροι γεωμετρικής προόδου
ΠΕΡΙΤΤΑ
τελευταία επεξεργασία από orestisgotsis σε Σάβ Φεβ 24, 2024 12:56 am, έχει επεξεργασθεί 1 φορά συνολικά.
Λέξεις Κλειδιά:
Re: Όροι γεωμετρικής προόδου
Θέτω :orestisgotsis έγραψε: ↑Σάβ Δεκ 02, 2023 8:05 pmΝα βρεθούν οιεάν αυτοί είναι διαδοχικοί όροι γεωμετρικής προόδου και ικανοποιούν
τις σχέσεις:και
.
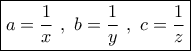 οπότε έχω το σύστημα:
οπότε έχω το σύστημα: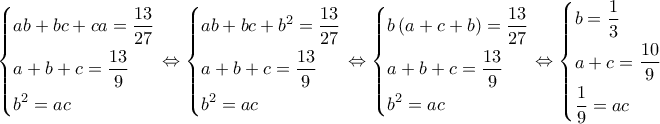
Οι δύο τελευταίες από τους τύπους του
 δίδουν την εξίσωση :
δίδουν την εξίσωση :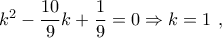 ή
ή 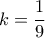 κι έτσι τελικά :
κι έτσι τελικά : 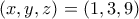 ή
ή 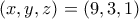
-
orestisgotsis
- Δημοσιεύσεις: 1753
- Εγγραφή: Σάβ Φεβ 25, 2012 10:19 pm
Re: Όροι γεωμετρικής προόδου
ΠΕΡΙΤΤΑ
τελευταία επεξεργασία από orestisgotsis σε Σάβ Φεβ 24, 2024 12:55 am, έχει επεξεργασθεί 1 φορά συνολικά.
Re: Όροι γεωμετρικής προόδου
Καλησπέρα...orestisgotsis έγραψε: ↑Σάβ Δεκ 02, 2023 8:05 pmΝα βρεθούν οιεάν αυτοί είναι διαδοχικοί όροι γεωμετρικής προόδου και ικανοποιούν
τις σχέσεις:και
.
Αφού τα τα μη μηδενικά
 είναι διαδοχικοί όροι γεωμ. προόδου, τότε θα είναι:
είναι διαδοχικοί όροι γεωμ. προόδου, τότε θα είναι: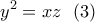
Οι εξισώσεις (1) και (2) γίνονται:
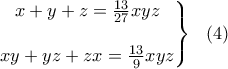
Σύμφωνα με την (3) το σύστημα (4) γίνεται:
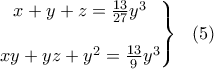
κι ακόμα:
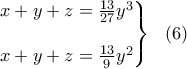
Εξισώνοντας τα δυο μέλη στο σύστημα (6) και επειδή
 προκύπτει
προκύπτει 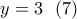
Από την πρώτη εξίσωση του συστήματος (6) θα είναι:
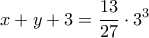
δηλαδή:
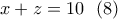
Θεωρώντας τους τρεις αυτούς όρους με τη μορφή:
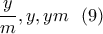
η εξίσωση (8) δίνει την εξίσωση:
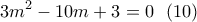
Εύκολα η (10) διαπιστώνεται ότι έχει δυο λύσεις. Αυτές είναι
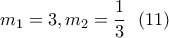
Από τις τιμές αυτές προκύπτει ότι έχουμε δυο τριάδιες ως λύση. Δηλαδή:
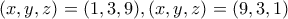
Σημείωση:
Χρησιμοποιώντας την
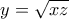
έχουμε το σύστημα:
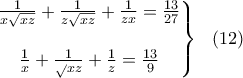
Το σύστημα αυτό το δίνουμε σε ένα λογισμικό, π.χ. το Maple και τότε έχουμε αμέσως τη λύση:
Κώστας Δόρτσιος
-
orestisgotsis
- Δημοσιεύσεις: 1753
- Εγγραφή: Σάβ Φεβ 25, 2012 10:19 pm
Re: Όροι γεωμετρικής προόδου
ΠΕΡΙΤΤΑ
τελευταία επεξεργασία από orestisgotsis σε Σάβ Φεβ 24, 2024 12:55 am, έχει επεξεργασθεί 2 φορές συνολικά.
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13301
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: Όροι γεωμετρικής προόδου
orestisgotsis έγραψε: ↑Σάβ Δεκ 02, 2023 8:05 pmΝα βρεθούν οιεάν αυτοί είναι διαδοχικοί όροι γεωμετρικής προόδου και ικανοποιούν
τις σχέσεις:και
.
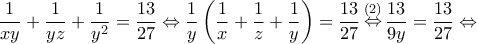
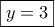
Από τη
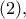
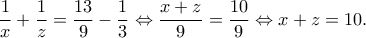 Άρα τα
Άρα τα 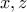 είναι ρίζες της εξίσωσης
είναι ρίζες της εξίσωσης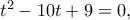 απ' όπου
απ' όπου 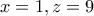 ή
ή 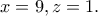
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες
