 είναι το πλήθος των θετικών διαιρετών του
είναι το πλήθος των θετικών διαιρετών του  να βρείτε όλα τα ακέραια
να βρείτε όλα τα ακέραια  για τα οποία ισχύει
για τα οποία ισχύει 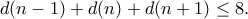
Ας δώσουμε προτεραιότητα σε μαθητές...
Συντονιστές: cretanman, silouan, rek2
 είναι το πλήθος των θετικών διαιρετών του
είναι το πλήθος των θετικών διαιρετών του  να βρείτε όλα τα ακέραια
να βρείτε όλα τα ακέραια  για τα οποία ισχύει
για τα οποία ισχύει 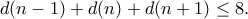
Αρχίζουμε με τον επόμενο Ισχυρισμό:
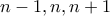 είναι πρώτος.
είναι πρώτος.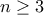 , είναι
, είναι 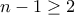 , οπότε είναι όλοι σύνθετοι, συνεπώς έχουν τουλάχιστον
, οπότε είναι όλοι σύνθετοι, συνεπώς έχουν τουλάχιστον  διαιρέτες έκαστος, οπότε συνολικά έχουμε
διαιρέτες έκαστος, οπότε συνολικά έχουμε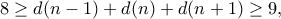

 είναι πρώτος. Ο
είναι πρώτος. Ο  σαφώς είναι δεκτός. Έστω τώρα ότι
σαφώς είναι δεκτός. Έστω τώρα ότι 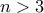 . Τότε, οι
. Τότε, οι  και
και  είναι άρτιοι (ο
είναι άρτιοι (ο 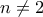 άρα περιττός), συνεπώς αφού
άρα περιττός), συνεπώς αφού  έχουν έκαστος τουλάχιστον τρεις διαιρέτες, και άρα
έχουν έκαστος τουλάχιστον τρεις διαιρέτες, και άρα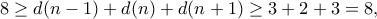
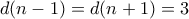 , που δίνει ότι
, που δίνει ότι 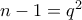 και
και 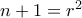 με
με  πρώτους. Αφού όμως είναι και οι δύο άρτιοι, έχουμε
πρώτους. Αφού όμως είναι και οι δύο άρτιοι, έχουμε 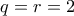 , άτοπο.
, άτοπο. είναι πρώτος. Έστω ότι
είναι πρώτος. Έστω ότι 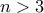 . Τότε ο
. Τότε ο  είναι άρτιος. Άρα,
είναι άρτιος. Άρα, 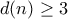 και
και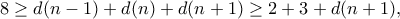
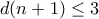 . Αν ο
. Αν ο  ήταν πρώτος, τότε
ήταν πρώτος, τότε 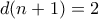 , άρα
, άρα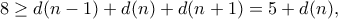
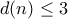 . Σαφώς, δεν γίνεται να είναι και ο
. Σαφώς, δεν γίνεται να είναι και ο  και ο
και ο  πρώτοι, οπότε
πρώτοι, οπότε 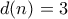 , που δίνει ότι
, που δίνει ότι 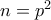 με
με  πρώτο, συνεπώς
πρώτο, συνεπώς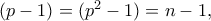
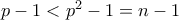 , είναι
, είναι 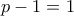 , που δίνει ότι
, που δίνει ότι  , που είναι δεκτός.
, που είναι δεκτός. δεν είναι πρώτος, τότε
δεν είναι πρώτος, τότε 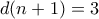 και
και 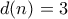 , οπότε
, οπότε 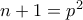 και
και 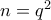 με
με  πρώτους, οπότε
πρώτους, οπότε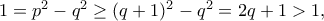
 είναι πρώτος. Τότε, είναι
είναι πρώτος. Τότε, είναι 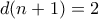 και όπως πριν,
και όπως πριν, 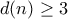 , συνεπώς
, συνεπώς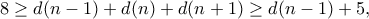
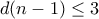 . Αν ο
. Αν ο  ήταν πρώτος, επιστρέφουμε στην προηγούμενη περίπτωση. Αν δεν είναι, τότε
ήταν πρώτος, επιστρέφουμε στην προηγούμενη περίπτωση. Αν δεν είναι, τότε 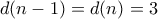 , οπότε οπως πριν έχουμε άτοπο.
, οπότε οπως πριν έχουμε άτοπο. ή
ή  .
.Αλλιώς.
 , έως 6, τα βρίσκουμε με το χέρι. Θα δούμε ότι δεν υπάρχουν άλλες λύσεις.
, έως 6, τα βρίσκουμε με το χέρι. Θα δούμε ότι δεν υπάρχουν άλλες λύσεις.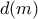 είναι
είναι 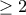 , πρέπει οι προσθετέοι της εξίσωσης να είναι ο καθένας
, πρέπει οι προσθετέοι της εξίσωσης να είναι ο καθένας  .
.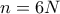 για
για 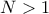 , τότε ο
, τότε ο  έχει διαιρέτες τους
έχει διαιρέτες τους 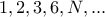 , δηλαδή περισσότερους από
, δηλαδή περισσότερους από  , άρα απορρίπτεται.
, άρα απορρίπτεται. 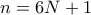 , τότε ο
, τότε ο  έχει διαιρέτες τους
έχει διαιρέτες τους 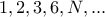 , και απορρίπτεται για τον ίδιο λόγο.
, και απορρίπτεται για τον ίδιο λόγο.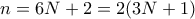 , τότε ο
, τότε ο  έχει διαιρέτες τους
έχει διαιρέτες τους 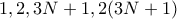 και o
και o 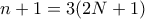 έχει διαιρέτες
έχει διαιρέτες 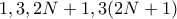 άρα απορρίπτεται γιατί περνάμε τους 8 (με τους δύο του
άρα απορρίπτεται γιατί περνάμε τους 8 (με τους δύο του  ).
). 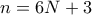 ,
, 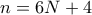 και
και 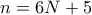 γιατί αν μετρήσουμε τους διαιρέτες των
γιατί αν μετρήσουμε τους διαιρέτες των 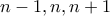 ξεπερνάμε τους
ξεπερνάμε τους  (άμεσο και στο ίδιο μήκος κύματος με τα προηγούμενα).
(άμεσο και στο ίδιο μήκος κύματος με τα προηγούμενα).Ας δούμε και αυτό:
 για τα οποία ισχύει
για τα οποία ισχύει 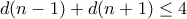
Mihalis_Lambrou έγραψε: ↑Κυρ Φεβ 20, 2022 11:17 pm
Ας δούμε και αυτό:
Να βρείτε όλα τα ακέραιαγια τα οποία ισχύει
Προσοχή, ή άσκηση είναι παγίδα.
Ουσιαστικά το νόημα της ερώτησης είναι γιατί λέω ότι η άσκηση είναι παγίδα. Και πρέπει να δείτε το όλο θέμα με χιούμορ...
 αλλά δεν θα πέσω στην παγίδα να προσπαθήσω να το αποδείξω.
αλλά δεν θα πέσω στην παγίδα να προσπαθήσω να το αποδείξω. Aκριβώς,Demetres έγραψε: ↑Κυρ Φεβ 20, 2022 11:37 pm
Πρέπει να υπάρχουν άπειρα τέτοιααλλά δεν θα πέσω στην παγίδα να προσπαθήσω να το αποδείξω.

Toικανοποιεί τη σχέση αν και μόνο αν τα
και
είναι και οι δύο πρώτοι. Δηλαδή το ζεύγος
είναι ζεύγος δίδυμων πρώτων
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες