 πίνακα είναι γραμμένος ένας αριθμός, εξάλλου κάθε αριθμός είναι ίσος με το γινόμενο όλων των αριθμών που βρίσκονται σε γειτονικά κατά πλευρά κελιά. Ποιό μπορεί να είναι το μέγιστο πλήθος διαφορετικών αριθμών σε αυτό το πίνακα;
πίνακα είναι γραμμένος ένας αριθμός, εξάλλου κάθε αριθμός είναι ίσος με το γινόμενο όλων των αριθμών που βρίσκονται σε γειτονικά κατά πλευρά κελιά. Ποιό μπορεί να είναι το μέγιστο πλήθος διαφορετικών αριθμών σε αυτό το πίνακα;Ίσα γινόμενα σε πίνακα
Συντονιστές: achilleas, emouroukos, silouan
- Al.Koutsouridis
- Δημοσιεύσεις: 1810
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Ίσα γινόμενα σε πίνακα
Σε κάθε κελί ενός  πίνακα είναι γραμμένος ένας αριθμός, εξάλλου κάθε αριθμός είναι ίσος με το γινόμενο όλων των αριθμών που βρίσκονται σε γειτονικά κατά πλευρά κελιά. Ποιό μπορεί να είναι το μέγιστο πλήθος διαφορετικών αριθμών σε αυτό το πίνακα;
πίνακα είναι γραμμένος ένας αριθμός, εξάλλου κάθε αριθμός είναι ίσος με το γινόμενο όλων των αριθμών που βρίσκονται σε γειτονικά κατά πλευρά κελιά. Ποιό μπορεί να είναι το μέγιστο πλήθος διαφορετικών αριθμών σε αυτό το πίνακα;
 πίνακα είναι γραμμένος ένας αριθμός, εξάλλου κάθε αριθμός είναι ίσος με το γινόμενο όλων των αριθμών που βρίσκονται σε γειτονικά κατά πλευρά κελιά. Ποιό μπορεί να είναι το μέγιστο πλήθος διαφορετικών αριθμών σε αυτό το πίνακα;
πίνακα είναι γραμμένος ένας αριθμός, εξάλλου κάθε αριθμός είναι ίσος με το γινόμενο όλων των αριθμών που βρίσκονται σε γειτονικά κατά πλευρά κελιά. Ποιό μπορεί να είναι το μέγιστο πλήθος διαφορετικών αριθμών σε αυτό το πίνακα;Λέξεις Κλειδιά:
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: Ίσα γινόμενα σε πίνακα
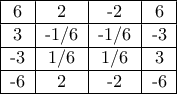
Δεν έχω κάποια «όμορφη» λύση. Ο πιο κάτω πίνακας δείχνει ότι μπορούμε να πετύχουμε τουλάχιστον  διαφορετικούς αριθμούς.
διαφορετικούς αριθμούς.
Θα δείξουμε ότι δεν μπορούμε να έχουμε περισσότερους. Γενικά ας υποθέσουμε ότι έχουμε τον πίνακα
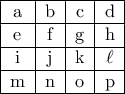
Αν υποθέσουμε ότι κάποιο είναι ίσο με , τότε είναι όλα
, τότε είναι όλα  , άτοπο. Αλλιώς, έχουμε τα εξής:
, άτοπο. Αλλιώς, έχουμε τα εξής:
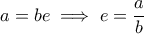
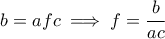
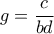 και
και  από συμμετρία.
από συμμετρία.
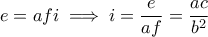
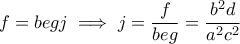
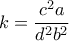 και
και 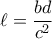 από συμμετρία.
από συμμετρία.
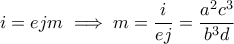
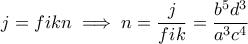
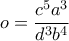 και
και 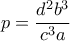 από συμμετρία.
από συμμετρία.
Επειδή όμως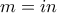 έχουμε
έχουμε 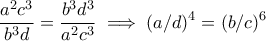
Επίσης,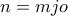 οπότε έχουμε
οπότε έχουμε 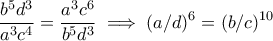
Άρα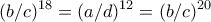 που δίνει
που δίνει 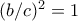 και
και 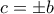 . Ομοίως
. Ομοίως 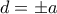 . Από τα πιο πάνω ο πίνακας γίνεται:
. Από τα πιο πάνω ο πίνακας γίνεται:
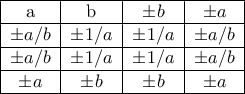
Παρατηρούμε ότι πράγματι έχουμε το πολύ διαφορετικούς αριθμούς. Τους
διαφορετικούς αριθμούς. Τους 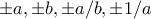 .
.
 διαφορετικούς αριθμούς.
διαφορετικούς αριθμούς.
Θα δείξουμε ότι δεν μπορούμε να έχουμε περισσότερους. Γενικά ας υποθέσουμε ότι έχουμε τον πίνακα

Αν υποθέσουμε ότι κάποιο είναι ίσο με
 , τότε είναι όλα
, τότε είναι όλα  , άτοπο. Αλλιώς, έχουμε τα εξής:
, άτοπο. Αλλιώς, έχουμε τα εξής: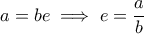

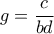 και
και  από συμμετρία.
από συμμετρία.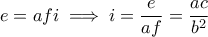
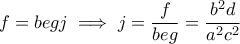
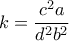 και
και 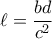 από συμμετρία.
από συμμετρία.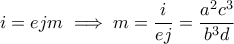
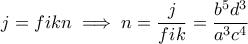
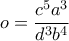 και
και 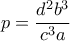 από συμμετρία.
από συμμετρία.Επειδή όμως
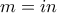 έχουμε
έχουμε 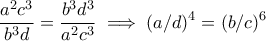
Επίσης,
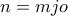 οπότε έχουμε
οπότε έχουμε 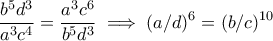
Άρα
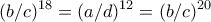 που δίνει
που δίνει 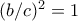 και
και 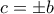 . Ομοίως
. Ομοίως 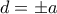 . Από τα πιο πάνω ο πίνακας γίνεται:
. Από τα πιο πάνω ο πίνακας γίνεται: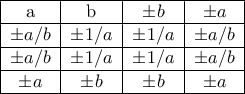
Παρατηρούμε ότι πράγματι έχουμε το πολύ
 διαφορετικούς αριθμούς. Τους
διαφορετικούς αριθμούς. Τους 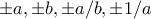 .
.Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης
