 , είναι :
, είναι :  και
και  το ύψος προς την υποτείνουσα .
το ύψος προς την υποτείνουσα .Έστω
 ένα άλλο σημείο της υποτείνουσας και
ένα άλλο σημείο της υποτείνουσας και  οι προβολές των
οι προβολές των  στην πλευρά
στην πλευρά  .
.α) Αν
 , βρείτε τη θέση του
, βρείτε τη θέση του  , ώστε :
, ώστε :  .
.β) Κάντε το ίδιο για οποιονδήποτε
 .
.Συντονιστές: silouan, Doloros, george visvikis
 , είναι :
, είναι :  και
και  το ύψος προς την υποτείνουσα .
το ύψος προς την υποτείνουσα . ένα άλλο σημείο της υποτείνουσας και
ένα άλλο σημείο της υποτείνουσας και  οι προβολές των
οι προβολές των  στην πλευρά
στην πλευρά  .
. , βρείτε τη θέση του
, βρείτε τη θέση του  , ώστε :
, ώστε :  .
. .
.Για την γενική περίπτωση. Έστω
 Με Π. Θ βρίσκω ότι
Με Π. Θ βρίσκω ότι  και
και 
 είναι όμοια:
είναι όμοια: 

 και λόγω ισεμβαδικότητας,
και λόγω ισεμβαδικότητας, 
 Η εξίσωση έχει δύο ρίζες. Η μία δίνει το
Η εξίσωση έχει δύο ρίζες. Η μία δίνει το  και η άλλη το
και η άλλη το 
 τότε
τότε  Στη συνέχεια προσδιορίζουμε το
Στη συνέχεια προσδιορίζουμε το  με κάθετη από το
με κάθετη από το  στην
στην 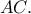
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες