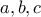 ισχύει:
ισχύει: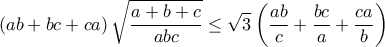
Από το Μαθηματικό Εργαστήρι ...
ΘέτουμεTolaso J Kos έγραψε: ↑Σάβ Φεβ 11, 2023 10:46 pmΝα δειχθεί ότι για θετικούς αριθμούςισχύει:
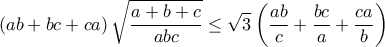
Από το Μαθηματικό Εργαστήρι ...
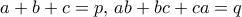 και
και  , οπότε αρκεί να αποδείξουμε ότι
, οπότε αρκεί να αποδείξουμε ότι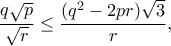
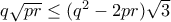 . Είναι,
. Είναι,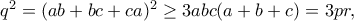 συνεπώς έχουμε ότι
συνεπώς έχουμε ότι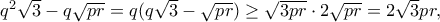
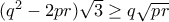 , που είναι το ζητούμενο.
, που είναι το ζητούμενο.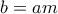 και
και 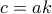 για κάποιους
για κάποιους 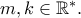 Η αποδεικτέα γίνεται :
Η αποδεικτέα γίνεται :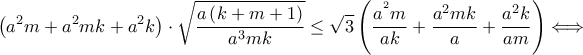
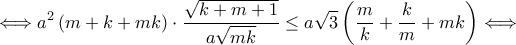
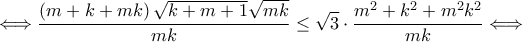
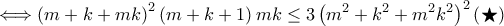
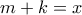 και
και 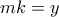 και γίνεται
και γίνεται 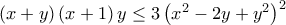 για θετικούς πραγματικούς η οποία γίνεται τετριμμένη.
για θετικούς πραγματικούς η οποία γίνεται τετριμμένη.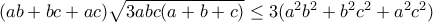
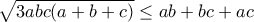
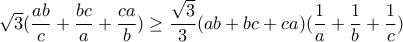
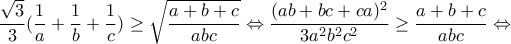
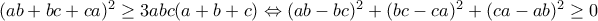 , που ισχύει.
, που ισχύει.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες