Έστω
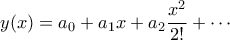 το ανάπτυγμα Taylor της
το ανάπτυγμα Taylor της  γύρω από το
γύρω από το  όπου
όπου 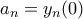 .
. Έχουμε
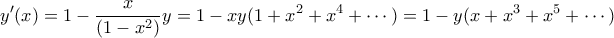
Συγκρίνοντας συντελεστές του
 έχουμε
έχουμε![\displaystyle \frac{y_{n+1}(0)}{n!} = -\left[\frac{y_{n-1}(0)}{(n-1)!} + \frac{y_{n-3}(0)}{(n-3)!} + \cdots \right] = -\frac{y_{n-1}(0)}{(n-1)!} + \frac{y_{n-1}(0)}{(n-2)!} \displaystyle \frac{y_{n+1}(0)}{n!} = -\left[\frac{y_{n-1}(0)}{(n-1)!} + \frac{y_{n-3}(0)}{(n-3)!} + \cdots \right] = -\frac{y_{n-1}(0)}{(n-1)!} + \frac{y_{n-1}(0)}{(n-2)!}](/forum/ext/geomar/texintegr/latexrender/pictures/bee2b783355c8c39470be3c191e3c345.png)
Παίρνουμε
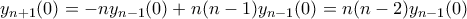
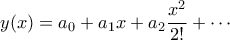 το ανάπτυγμα Taylor της
το ανάπτυγμα Taylor της  γύρω από το
γύρω από το  όπου
όπου 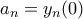 .
. 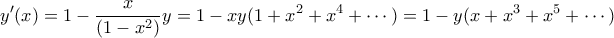
 έχουμε
έχουμε![\displaystyle \frac{y_{n+1}(0)}{n!} = -\left[\frac{y_{n-1}(0)}{(n-1)!} + \frac{y_{n-3}(0)}{(n-3)!} + \cdots \right] = -\frac{y_{n-1}(0)}{(n-1)!} + \frac{y_{n-1}(0)}{(n-2)!} \displaystyle \frac{y_{n+1}(0)}{n!} = -\left[\frac{y_{n-1}(0)}{(n-1)!} + \frac{y_{n-3}(0)}{(n-3)!} + \cdots \right] = -\frac{y_{n-1}(0)}{(n-1)!} + \frac{y_{n-1}(0)}{(n-2)!}](/forum/ext/geomar/texintegr/latexrender/pictures/bee2b783355c8c39470be3c191e3c345.png)
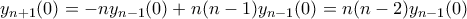
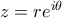 μη μηδενικός μιγαδικός αριθμός στην κανονική του μορφή. Αν ο
μη μηδενικός μιγαδικός αριθμός στην κανονική του μορφή. Αν ο 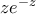 είναι πραγματικός, να αποδείξετε ότι ο αριθμός
είναι πραγματικός, να αποδείξετε ότι ο αριθμός 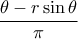
.Mihalis_Lambrou έγραψε: ↑Τρί Δεκ 27, 2022 10:38 pmΆσκηση 16 (Special paper, Ιούνιος 1974) .
(i) ... (Το αφήνω ως ρουτίνα).
(ii) Έστωμη μηδενικός μιγαδικός αριθμός στην κανονική του μορφή. Αν ο
είναι πραγματικός, να αποδείξετε ότι ο αριθμός
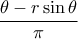
είναι ακέραιος.
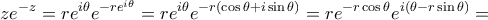
![\displaystyle{= re^{-r\cos \theta } \left [ \cos (\theta -r\sin \theta) +i \sin (\theta -r\sin \theta)\right ] } \displaystyle{= re^{-r\cos \theta } \left [ \cos (\theta -r\sin \theta) +i \sin (\theta -r\sin \theta)\right ] }](/forum/ext/geomar/texintegr/latexrender/pictures/5e9d946800ceda744437f61ffe56ff4b.png)
 , και άρα
, και άρα 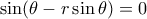 . Συνεπώς για κάποιο
. Συνεπώς για κάποιο  ακέραιο είναι
ακέραιο είναι 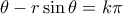 , από όπου το ζητούμενο.
, από όπου το ζητούμενο. και έστω
και έστω ![f:[0,\,p] \longrightarrow \mathbb R f:[0,\,p] \longrightarrow \mathbb R](/forum/ext/geomar/texintegr/latexrender/pictures/673f6c0a2f206c39bcacbbafc6c14f1f.png) μία συνεχής συνάρτηση που για κάθε
μία συνεχής συνάρτηση που για κάθε ![x\in [0,\, p] x\in [0,\, p]](/forum/ext/geomar/texintegr/latexrender/pictures/acc057bb680790c1ffe86f4584aa7895.png) ικανοποιεί
ικανοποιεί 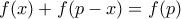 . Δείξτε ότι
. Δείξτε ότι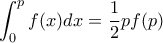
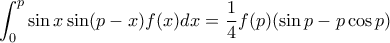
Mihalis_Lambrou έγραψε: ↑Πέμ Ιαν 05, 2023 7:27 pmΆσκηση 17 (Special paper, Ιούνιος 1980) .
(i) Έστωκαι έστω
μία συνεχής συνάρτηση που για κάθε
ικανοποιεί
. Δείξτε ότι
α)
β)
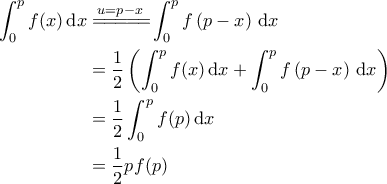
![\displaystyle{\begin{aligned}
\int_{0}^{p} \sin x \sin \left ( p-x \right ) f(x)\, \mathrm{d}x &\overset{u=p-x}{=\! =\! =\! =\! =\!} \int_{0}^{p} \sin x \sin \left ( p- x \right ) f \left ( p-x \right )\, \mathrm{d}x \\
&=\frac{1}{2} \int_{0}^{p} \left [ \sin x \sin \left ( p-x \right ) f(x) + \sin x \sin \left ( p- x \right ) f \left ( p-x \right ) \right ]\, \mathrm{d}x \\
&=\frac{1}{2} \int_{0}^{p} \sin x \sin \left ( p-x \right ) \left [ f (x) + f (p-x) \right ] \, \mathrm{d}x \\
&=\frac{f(p)}{2} \int_{0}^{p} \sin x \sin \left ( p-x \right )\, \mathrm{d}x \\
&= \frac{p f(p)}{4} \left ( \sin p - p \cos p \right )
\end{aligned}} \displaystyle{\begin{aligned}
\int_{0}^{p} \sin x \sin \left ( p-x \right ) f(x)\, \mathrm{d}x &\overset{u=p-x}{=\! =\! =\! =\! =\!} \int_{0}^{p} \sin x \sin \left ( p- x \right ) f \left ( p-x \right )\, \mathrm{d}x \\
&=\frac{1}{2} \int_{0}^{p} \left [ \sin x \sin \left ( p-x \right ) f(x) + \sin x \sin \left ( p- x \right ) f \left ( p-x \right ) \right ]\, \mathrm{d}x \\
&=\frac{1}{2} \int_{0}^{p} \sin x \sin \left ( p-x \right ) \left [ f (x) + f (p-x) \right ] \, \mathrm{d}x \\
&=\frac{f(p)}{2} \int_{0}^{p} \sin x \sin \left ( p-x \right )\, \mathrm{d}x \\
&= \frac{p f(p)}{4} \left ( \sin p - p \cos p \right )
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/d000a4bee19925cfa13c77a943a8e5fb.png)

 συνεχής συνάρτηση. Δείξτε ότι
συνεχής συνάρτηση. Δείξτε ότι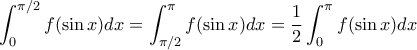
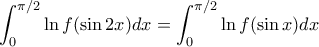 .
.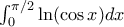
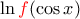 ενώ το σωστό είναι χωρίς το
ενώ το σωστό είναι χωρίς το  .
.  . Όμως την αφήνω όπως είναι παραπάνω γιατί τυχαίνει να είναι σωστή, με μόνη προσθήκη οι τιμές της
. Όμως την αφήνω όπως είναι παραπάνω γιατί τυχαίνει να είναι σωστή, με μόνη προσθήκη οι τιμές της  να είναι θετικές (για να έχει νόημα ο λογάριθμος).
να είναι θετικές (για να έχει νόημα ο λογάριθμος).Mihalis_Lambrou έγραψε: ↑Παρ Ιαν 06, 2023 11:44 amΆσκηση 18 (Special paper, Ιούνιος 1985) .
α) (το αφήνω ως ρουτίνα).
β) Έστωσυνεχής συνάρτηση. Δείξτε ότι
Από αυτά, ή αλλιώς, δείξτε ότι
.
Με χρήση αυτού να βρείτε τo
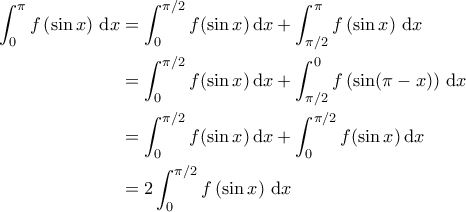
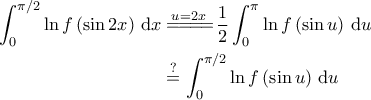
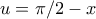 το φέρνει στο ολοκλήρωμα
το φέρνει στο ολοκλήρωμα 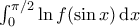 . Αρκεί;
. Αρκεί;
Έστωσυνεχής συνάρτηση. Να δειχθεί ότι:
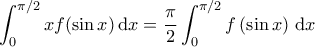

'
'Tolaso J Kos έγραψε: ↑Παρ Ιαν 06, 2023 9:18 pm... Για το τελευταίο ερώτημα δε ξέρω τι πρέπει να απαντήσω. Η αλλαγή μεταβλητήςτο φέρνει στο ολοκλήρωμα
. Αρκεί;
 και τον
και τον  .
.
Ωχχχχ. Έχεις δίκιο. Υπάρχει ένα παραπανήσιο
 .
.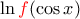 ενώ το σωστό είναι χωρίς το
ενώ το σωστό είναι χωρίς το  .
.  . Όμως την αφήνω όπως είναι παραπάνω γιατί τυχαίνει να είναι σωστή, με μόνη προσθήκη οι τιμές της
. Όμως την αφήνω όπως είναι παραπάνω γιατί τυχαίνει να είναι σωστή, με μόνη προσθήκη οι τιμές της  να είναι θετικές (για να έχει νόημα ο λογάριθμος).
να είναι θετικές (για να έχει νόημα ο λογάριθμος).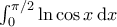 . Σωστά; Τότε,
. Σωστά; Τότε,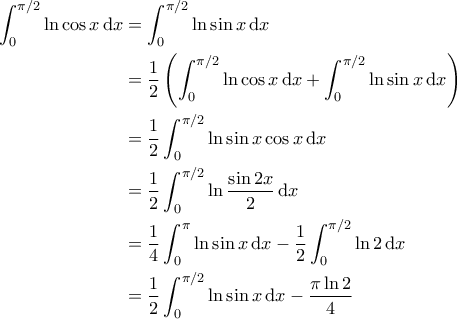
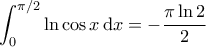 .
.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης