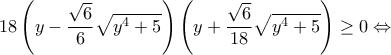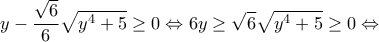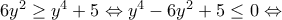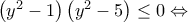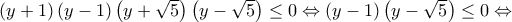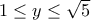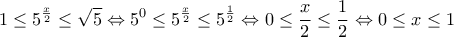3. Να λύσετε την ανίσωση
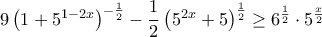 .
.4. Να λύσετε την εξίσωση
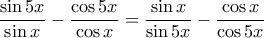 .
.5. Στις
 από το χωριό Άνω Ποταμιά με την φορά της ροής του ποταμού προς τα κάτω στο χωριό Κάτω Ποταμιά ξεκίνησε το σκάφος "Αστραπή". Όταν έφτασε στα
από το χωριό Άνω Ποταμιά με την φορά της ροής του ποταμού προς τα κάτω στο χωριό Κάτω Ποταμιά ξεκίνησε το σκάφος "Αστραπή". Όταν έφτασε στα  μέτρα από την Κάτω Ποταμία, ξεκίνησε για να το συναντήσει από την Κάτω Ποταμιά το σκάφος "Θάρρος". Ακριβώς αυτή την χρονική στιγμή η "Αστραπή", μη έχων σκοπό να συνατήση το "Θάρρος", έκανε αναστροφή και κατευθύνθηκε προς την Άνω Ποταμιά. Στις
μέτρα από την Κάτω Ποταμία, ξεκίνησε για να το συναντήσει από την Κάτω Ποταμιά το σκάφος "Θάρρος". Ακριβώς αυτή την χρονική στιγμή η "Αστραπή", μη έχων σκοπό να συνατήση το "Θάρρος", έκανε αναστροφή και κατευθύνθηκε προς την Άνω Ποταμιά. Στις 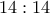 , όταν η απόσταση στο ποτάμι από την Αστραπή στην Άνω Ποταμιά έγινε ίση με την απόσταση στο ποτάμι από το Θάρρος στην Αστραπή, στο Θάρρος συνειδητοποίησαν ότι κινούνται με την ίδια ταχύτητα με την Αστραπή, έκαναν αναστοφή και κατευθύνθηκαν πίσω στην Κάτω Ποταμιά. Στις αρχικές τους θέσεις τα σκάφη επέστρεψαν ταυτόχρονα στις
, όταν η απόσταση στο ποτάμι από την Αστραπή στην Άνω Ποταμιά έγινε ίση με την απόσταση στο ποτάμι από το Θάρρος στην Αστραπή, στο Θάρρος συνειδητοποίησαν ότι κινούνται με την ίδια ταχύτητα με την Αστραπή, έκαναν αναστοφή και κατευθύνθηκαν πίσω στην Κάτω Ποταμιά. Στις αρχικές τους θέσεις τα σκάφη επέστρεψαν ταυτόχρονα στις 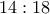 . Να βρείτε την απόσταση στο ποτάμι μεταξύ των Άνω και Κάτω Ποταμιάς, αν είναι γνωστό, ότι και τα δυο σκάφη κάνουν ομαλή κίνηση με ίσες ιδίες ταχύτητες.
. Να βρείτε την απόσταση στο ποτάμι μεταξύ των Άνω και Κάτω Ποταμιάς, αν είναι γνωστό, ότι και τα δυο σκάφη κάνουν ομαλή κίνηση με ίσες ιδίες ταχύτητες. 6. Το τραπέζιο
 είναι εγγεγραμμένο σε κύκλο ακτίνας
είναι εγγεγραμμένο σε κύκλο ακτίνας  και περιγεγραμμένο σε κύκλο ακτίνας
και περιγεγραμμένο σε κύκλο ακτίνας  . Να βρείτε την ακτίνα
. Να βρείτε την ακτίνα  , αν
, αν 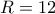 και το συνημίτονο της γωνίας μεταξύ της διαγωνίου
και το συνημίτονο της γωνίας μεταξύ της διαγωνίου  και της βάσης
και της βάσης  είναι ίσο με
είναι ίσο με  .
.7. Η βάση ορθού πρίσματος
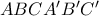 είναι ορθογώνιο τρίγωνο
είναι ορθογώνιο τρίγωνο  , με
, με  . Στην ακμή
. Στην ακμή  της άνω βάσης (παράλληλης προς την
της άνω βάσης (παράλληλης προς την  ) δίνεται σημείο
) δίνεται σημείο  τέτοιο, ώστε
τέτοιο, ώστε 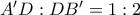 . Να βρείτε την ακτίνα της εγγεγραμμένης σφαίρας στο τετράεδρο
. Να βρείτε την ακτίνα της εγγεγραμμένης σφαίρας στο τετράεδρο 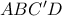 , αν το ύψος του πρίσματος είναι 1.
, αν το ύψος του πρίσματος είναι 1.8. Να βρείτε όλες τις τιμές της παραμέτρου
 , για τις οποίες η εξίσωση
, για τις οποίες η εξίσωση 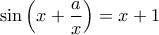
έχει άπειρες λύσεις.
Μια άλλη έκδοση του θέματος 8:
8. Να βρείτε όλες τις τιμές της παραμέτρου
 , για τις οποίες η εξίσωση
, για τις οποίες η εξίσωση 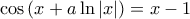
έχει άπειρες λύσεις.
Edit: 24/06/2023 Διόρθωση στην εκφώνηση της 6ης άσκησης. Ευχαριστώ τον κ.Τηλέμαχο (ΚΕΦΑΛΟΝΙΤΗΣ) για την παρατήρηση.



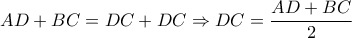
 συναρτήσει της ακτίνας
συναρτήσει της ακτίνας 
 η γωνία που σχηματίζουν οι
η γωνία που σχηματίζουν οι 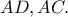
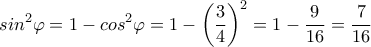
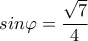
 προκύπτει ότι
προκύπτει ότι 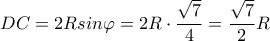
 η προβολή του
η προβολή του  επί της
επί της 
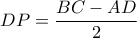
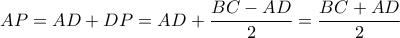
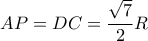
 το οποίο είναι ίσο με
το οποίο είναι ίσο με 
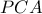 έχουμε ότι
έχουμε ότι 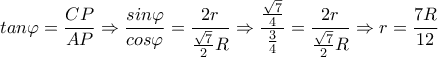

 λεπτά, η ταχύτητα ανόδου των πλοίων είναι
λεπτά, η ταχύτητα ανόδου των πλοίων είναι 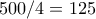 μέτρα ανά λεπτό.
μέτρα ανά λεπτό. η απόσταση των χωριών,
η απόσταση των χωριών,  η ταχύτητα καθόδου των πλοίων και
η ταχύτητα καθόδου των πλοίων και 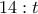 η ώρα που η αστραπή φθάνει στο σημείο που έκανε αναστροφή.
η ώρα που η αστραπή φθάνει στο σημείο που έκανε αναστροφή.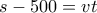 .
. 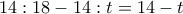 λεπτά με ταχύτητα
λεπτά με ταχύτητα  μέτρα ανά λεπτό, διανύοντας απόσταση
μέτρα ανά λεπτό, διανύοντας απόσταση 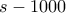 , επομένως
, επομένως 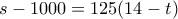
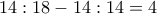 λεπτά με ταχύτητα
λεπτά με ταχύτητα 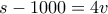
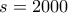 μέτρα. (t=6 ή t=12 κ.λπ.)
μέτρα. (t=6 ή t=12 κ.λπ.)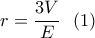
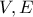 είναι ο όγκος και η επιφάνεια της τριγωνικής πυραμίδας
είναι ο όγκος και η επιφάνεια της τριγωνικής πυραμίδας 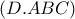 .
.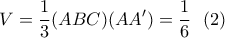

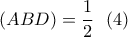
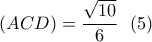
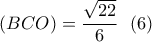
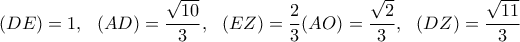
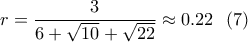
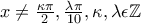
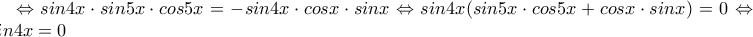 ή
ή 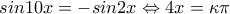 ή
ή 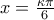 ή
ή 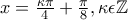 , που είναι δεκτές.
, που είναι δεκτές.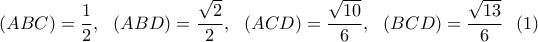

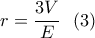
 είναι το εμβαδόν των τεσσάρων εδρών της πυραμίδας.
είναι το εμβαδόν των τεσσάρων εδρών της πυραμίδας. 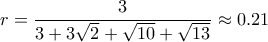
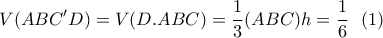
 στο σημείο
στο σημείο  ο όγκος αυτής δεν μεταβάλλεται.
ο όγκος αυτής δεν μεταβάλλεται.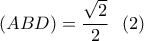
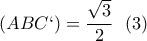
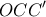 )
)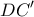
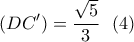
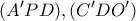 βρίσκουμε:
βρίσκουμε: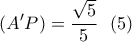
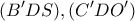 βρίσκουμε:
βρίσκουμε:
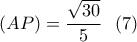
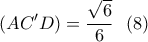
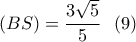
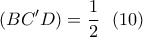
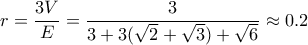
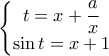 (1)
(1) , προκύπτει άλλη μια εξίσωση
, προκύπτει άλλη μια εξίσωση 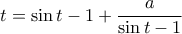 (2)
(2)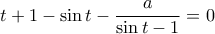 (3)
(3)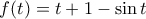 . Αυτή ορίζεται και είναι συνεχής σε όλη την ευθεία των πραγματικών αριθμών. Η παράγωγός της
. Αυτή ορίζεται και είναι συνεχής σε όλη την ευθεία των πραγματικών αριθμών. Η παράγωγός της 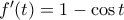 είναι μη αρνητική και μηδενίζεται στα σημεία της μορφής
είναι μη αρνητική και μηδενίζεται στα σημεία της μορφής 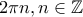 . Από τα παραπάνω συμπεράνουμε, ότι η
. Από τα παραπάνω συμπεράνουμε, ότι η 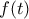 είναι γνησίως αύξουσα σε κάθε διάστημα
είναι γνησίως αύξουσα σε κάθε διάστημα ![\left [ 2 \pi n, 2 \pi (n+1) \right ], n \in \mathbb{Z} \left [ 2 \pi n, 2 \pi (n+1) \right ], n \in \mathbb{Z}](/forum/ext/geomar/texintegr/latexrender/pictures/0ea9c5ffa2cf378d961846416f7128ab.png) και άρα η
και άρα η 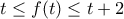 προκύπτει, ότι το σύνολο τιμών αυτής της συνάρτησης είναι όλη η ευθεία των πραγματικών αριθμών.
προκύπτει, ότι το σύνολο τιμών αυτής της συνάρτησης είναι όλη η ευθεία των πραγματικών αριθμών.  . Τότε η εξίσωση (3) παίρνει την μορφή
. Τότε η εξίσωση (3) παίρνει την μορφή  . Έχοντας υπόψη την μονοτονία της συνάρτησης
. Έχοντας υπόψη την μονοτονία της συνάρτησης  . Στο δίάστημα
. Στο δίάστημα ![\left [\dfrac{\pi}{2} +2 \pi k, \dfrac{3\pi}{2}+2 \pi k \right ] \left [\dfrac{\pi}{2} +2 \pi k, \dfrac{3\pi}{2}+2 \pi k \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/fe51fba2bd7a3596bab72162010e559e.png) για οποιονδήποτε ακέραιο
για οποιονδήποτε ακέραιο  η συνάρτηση
η συνάρτηση  είναι γνησίως φθίνουσα από το
είναι γνησίως φθίνουσα από το  έως το
έως το  . Άρα η συνάρτηση
. Άρα η συνάρτηση 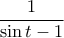 είναι γνησιώς αύξουσα από το
είναι γνησιώς αύξουσα από το 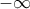 έως το
έως το  και η συνάρτηση
και η συνάρτηση 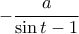 είναι γνησίως αύξουσα από το
είναι γνησίως αύξουσα από το  έως το
έως το  . Ως άθροισμα δυο γνησίως αύξουσων συναρτήσεων, το αριστερό μέλος της εξίσωσης (3) θα είναι και αυτό γνησίως αύξουσα συνάρτηση στο διάστημα
. Ως άθροισμα δυο γνησίως αύξουσων συναρτήσεων, το αριστερό μέλος της εξίσωσης (3) θα είναι και αυτό γνησίως αύξουσα συνάρτηση στο διάστημα  έως το
έως το 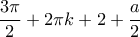 . Άρα, για οποιονδήποτε ακέραιο
. Άρα, για οποιονδήποτε ακέραιο 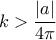 το αριστερό μέλος της (3) λαμβάνει στο διάστημα
το αριστερό μέλος της (3) λαμβάνει στο διάστημα  τόσο αρνητικές, όσο και θετικές τιμές. Εφόσον είναι συνεχής σε αυτό το διάστημα σε κάποιο σημείο αυτού του διαστήματος θα μηδενίζεται, δηλαδή σε αυτό διάστημα η εξίσωση (3) έχει λύση. Τότε όμως το σύνολο των λύσων της εξίσωσης (3) και της αρχικής εξίσωσης είναι άπειρο.
τόσο αρνητικές, όσο και θετικές τιμές. Εφόσον είναι συνεχής σε αυτό το διάστημα σε κάποιο σημείο αυτού του διαστήματος θα μηδενίζεται, δηλαδή σε αυτό διάστημα η εξίσωση (3) έχει λύση. Τότε όμως το σύνολο των λύσων της εξίσωσης (3) και της αρχικής εξίσωσης είναι άπειρο. . Σε αυτήν την περίπτωση ο συλλογισμός είναι όμοιως με την προηγούμενη. Στο διάστημα
. Σε αυτήν την περίπτωση ο συλλογισμός είναι όμοιως με την προηγούμενη. Στο διάστημα ![\left [-\dfrac{\pi}{2} +2 \pi k, \dfrac{\pi}{2}+2 \pi k \right ] \left [-\dfrac{\pi}{2} +2 \pi k, \dfrac{\pi}{2}+2 \pi k \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/df4dbc71dc5ea128593efd51e20fe0e6.png) για οποιονδήποτε ακέραιο
για οποιονδήποτε ακέραιο  είναι γνησίως αύξουσα από το
είναι γνησίως αύξουσα από το  . Ως άθροισμα δυο γνησίως αύξουσων συναρτήσεων, το αριστερό μέλος της εξίσωσης (3) θα είναι και αυτή γνησίως αύξουσα συνάρτηση στο διάστημα
. Ως άθροισμα δυο γνησίως αύξουσων συναρτήσεων, το αριστερό μέλος της εξίσωσης (3) θα είναι και αυτή γνησίως αύξουσα συνάρτηση στο διάστημα 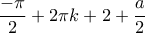 έως το
έως το 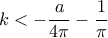 το αριστερό μέλος της (3) θα λαμβάνει στο διάστημα
το αριστερό μέλος της (3) θα λαμβάνει στο διάστημα 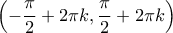 τόσο αρνητικές, όσο και θετικές τιμές. Εφόσον είναι συνεχής σε αυτό το διάστημα σε κάποιο σημείο αυτού του διαστήματος θα μηδενίζεται, δηλαδή σε αυτό διάστημα η εξίσωση (3) έχει λύση. Τότε όμως το σύνολο των λύσων της εξίσωσης (3) και της αρχικής εξίσωσης είναι άπειρο.
τόσο αρνητικές, όσο και θετικές τιμές. Εφόσον είναι συνεχής σε αυτό το διάστημα σε κάποιο σημείο αυτού του διαστήματος θα μηδενίζεται, δηλαδή σε αυτό διάστημα η εξίσωση (3) έχει λύση. Τότε όμως το σύνολο των λύσων της εξίσωσης (3) και της αρχικής εξίσωσης είναι άπειρο. .
.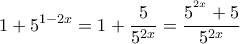
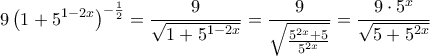
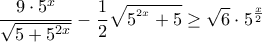
 και έτσι
και έτσι 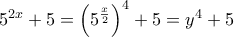
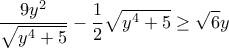 που ισοδυναμεί με
που ισοδυναμεί με 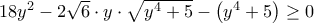 η οποία ισοδυναμεί με
η οποία ισοδυναμεί με