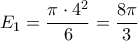ορίζονται δυο ευθείες
ορίζονται δυο ευθείες 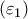 και
και 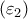 και εκτός του
και εκτός του  δυο σημεία
δυο σημεία  και
και  . Από το σημείο τομής
. Από το σημείο τομής  της
της  και του επιπέδου
και του επιπέδου  , φέρνουμε τυχαία ευθεία
, φέρνουμε τυχαία ευθεία  αντίστοιχα τις
αντίστοιχα τις 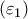 και
και 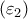 στα σημεία
στα σημεία  και
και  . Έστω
. Έστω  η τομή των
η τομή των 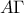 και
και  ,
,  η τομή των
η τομή των 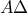 και
και  . Ζητούνται :
. Ζητούνται :α) Να βρεθούν οι γεωμετρικοί τόποι των σημείων
 και
και  όταν η
όταν η  περιστρέφεται στο επίπεδο
περιστρέφεται στο επίπεδο  γύρω από το
γύρω από το 
β) Να δειχθεί οτι η
 ορίζει πάνω στην
ορίζει πάνω στην  σταθερό σημείο.
σταθερό σημείο.2. Δίνονται δυο κύκλοι
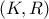 και
και 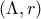 και φέρνουμε δυο τυχαίες εξωτερικές εφαπτόμενες τους
και φέρνουμε δυο τυχαίες εξωτερικές εφαπτόμενες τους  και
και  τεμνόμενες κάθετα στο
τεμνόμενες κάθετα στο  , δηλαδή
, δηλαδή 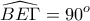 . Από τα
. Από τα  και
και  φέρνουμε δυο ευθείες
φέρνουμε δυο ευθείες 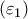 και
και 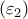 παράλληλες αντίστοιχα προς τις
παράλληλες αντίστοιχα προς τις  και
και  .
.Να δειχτεί οτι:
α) η διχοτόμος της ορθής γωνίας των εφαπτομένων και η διχοτόμος της ορθής γωνίας των
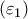 και
και 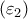 , έχουν μεταξύ τους σταθερή απόσταση ανεξάρτητη από την θέση των εφαπτομένων
, έχουν μεταξύ τους σταθερή απόσταση ανεξάρτητη από την θέση των εφαπτομένωνβ) η διχοτόμος των εφαπτομένων εφάπτεται σταθερού κύκλου
3. Να βρεθεί ο γεωμετρικός τόπος των σημείων
 επιπέδου
επιπέδου  , των οποίων οι αποστάσεις
, των οποίων οι αποστάσεις 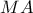 και
και 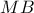 από δυο δοθέντα σημεία
από δυο δοθέντα σημεία  και
και  έχουν λόγο ίσον προς
έχουν λόγο ίσον προς 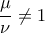 . Έστω
. Έστω 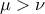 .
.4. Να βρεθεί η επιφάνεια
 σφαίρας O εγγεγραμμένης σε κανονικό τετράεδρο
σφαίρας O εγγεγραμμένης σε κανονικό τετράεδρο 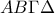 ακμής
ακμής 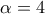 εκατοστά.
εκατοστά.
 ένα σημείο του γεωμετρικού τόπου. Φέρνω τις διχοτόμους της εσωτερικής και εξωτερικής γωνίας
ένα σημείο του γεωμετρικού τόπου. Φέρνω τις διχοτόμους της εσωτερικής και εξωτερικής γωνίας 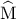 που τέμνουν την
που τέμνουν την  στα σημεία
στα σημεία 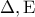 αντίστοιχα. Από τα θεωρήματα διχοτόμων έχουμε:
αντίστοιχα. Από τα θεωρήματα διχοτόμων έχουμε: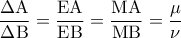 .
.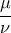 και είναι μοναδικά. Επομένως το τμήμα
και είναι μοναδικά. Επομένως το τμήμα  είναι σταθερό και φαίνεται από το σημείο
είναι σταθερό και φαίνεται από το σημείο  και διαιρούμε το
και διαιρούμε το  ένα σημείο του κύκλου με διάμετρο τη
ένα σημείο του κύκλου με διάμετρο τη 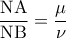 .
. ευθεία παράλληλη στη
ευθεία παράλληλη στη 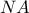 που τέμνει τις ευθείες
που τέμνει τις ευθείες 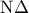 και
και  στα σημεία
στα σημεία  και
και  αντίστοιχα. Τα τρίγωνα
αντίστοιχα. Τα τρίγωνα 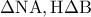 καθώς επίσης και τα
καθώς επίσης και τα 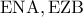 έχουν τις πλευρές τους ανάλογες. Άρα:
έχουν τις πλευρές τους ανάλογες. Άρα: 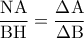 \displaystyle{\displaystyle{ = \frac{\mu }{\nu }}
\displaystyle{\displaystyle{ = \frac{\mu }{\nu }} \displaystyle{\frac{{{\rm N}{\rm A}}}{{{\rm B}{\rm Z}}} = \frac{{{\rm E}{\rm A}}}{{{\rm E}{\rm B}}}}}
\displaystyle{\frac{{{\rm N}{\rm A}}}{{{\rm B}{\rm Z}}} = \frac{{{\rm E}{\rm A}}}{{{\rm E}{\rm B}}}}}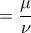 . Από αυτές τις σχέσεις προκύπτει ότι
. Από αυτές τις σχέσεις προκύπτει ότι 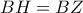 .
.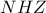 είναι ορθογώνιο (η
είναι ορθογώνιο (η  είναι διάμεσος. Άρα
είναι διάμεσος. Άρα 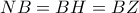 . Οπότε
. Οπότε 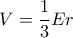 , όπου
, όπου  o όγκος του κανονικού τετραέδρου,
o όγκος του κανονικού τετραέδρου,  η ολική επιφάνεια του κανονικού τετραέδρου και
η ολική επιφάνεια του κανονικού τετραέδρου και  η ακτίνα της σφαίρας που είναι εγγεγραμμένη στο κανονικό τετράεδρο.
η ακτίνα της σφαίρας που είναι εγγεγραμμένη στο κανονικό τετράεδρο.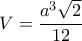 και
και 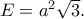
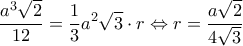
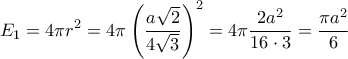
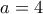 προκύπτει ότι
προκύπτει ότι