Μαθηματικά κατεύθυνσης 2014
Re: Μαθηματικά κατεύθυνσης 2014
Ευφυέστατη η λύση του Δ3 με Θεώρημα Μέγιστης και Ελάχιστης Τιμής.
ΜΠΡΑΒΟ!!!!!
ΜΠΡΑΒΟ!!!!!
Re: Μαθηματικά κατεύθυνσης 2014
Το θέμα Δ3 αλλιώς...
Έχουμε![g'\left( x \right) = 2\left( {{e^x} - e} \right)\left( {x - 2} \right)\left[ {\left( {x - 1} \right){e^x} - e} \right] g'\left( x \right) = 2\left( {{e^x} - e} \right)\left( {x - 2} \right)\left[ {\left( {x - 1} \right){e^x} - e} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/2137b5a9adf241151e4697f3266f6fd0.png)
και για κάθε
για κάθε  . Από θεώρημα Rolle στο [1,2] υπάρχει
. Από θεώρημα Rolle στο [1,2] υπάρχει 
τέτοιο ώστε η οποία είναι ρίζα αναγκαστικά της συνάρτησης
η οποία είναι ρίζα αναγκαστικά της συνάρτησης  και παρατηρώ ότι
και παρατηρώ ότι 
Δηλαδή η h είναι γνησίως αύξουσα στο με αποτέλεσμα το ξ να είναι μοναδική της ρίζα. Τελικά η
με αποτέλεσμα το ξ να είναι μοναδική της ρίζα. Τελικά η  έχει ακριβώς τρεις ρίζες.
έχει ακριβώς τρεις ρίζες.
Έχουμε: συνεχής ως πράξεις συνεχών, συνεπώς διατηρεί πρόσημο στα διαφορετικά διαστήματα που χωρίζουν οι ρίζες της το
συνεχής ως πράξεις συνεχών, συνεπώς διατηρεί πρόσημο στα διαφορετικά διαστήματα που χωρίζουν οι ρίζες της το 
Η ικανοποιεί τις προυποθέσεις του Θ.Μ.Τ στα διαστήματα [1,ξ] και [ξ,2] συνεπώς υπάρχουν
ικανοποιεί τις προυποθέσεις του Θ.Μ.Τ στα διαστήματα [1,ξ] και [ξ,2] συνεπώς υπάρχουν  με
με 
τέτοια ώστε: και
και

Συνεπώς για έχουμε
έχουμε  και για
και για  έχουμε
έχουμε  .
.
Το πρόσημο της στα διαστήματα
στα διαστήματα  και
και  βρίσκεται εύκολα.
βρίσκεται εύκολα.
Παρατήρηση: Παρόμοια άσκηση υπάρχει στο σχολικό βιβλίο σελ. 270 (άσκηση 6 Β΄Ομ) και τη θεωρώ μια από τις ωραιότερες της ενότητας.
Έχουμε
![g'\left( x \right) = 2\left( {{e^x} - e} \right)\left( {x - 2} \right)\left[ {\left( {x - 1} \right){e^x} - e} \right] g'\left( x \right) = 2\left( {{e^x} - e} \right)\left( {x - 2} \right)\left[ {\left( {x - 1} \right){e^x} - e} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/2137b5a9adf241151e4697f3266f6fd0.png)
και
 για κάθε
για κάθε  . Από θεώρημα Rolle στο [1,2] υπάρχει
. Από θεώρημα Rolle στο [1,2] υπάρχει 
τέτοιο ώστε
 η οποία είναι ρίζα αναγκαστικά της συνάρτησης
η οποία είναι ρίζα αναγκαστικά της συνάρτησης  και παρατηρώ ότι
και παρατηρώ ότι 
Δηλαδή η h είναι γνησίως αύξουσα στο
 με αποτέλεσμα το ξ να είναι μοναδική της ρίζα. Τελικά η
με αποτέλεσμα το ξ να είναι μοναδική της ρίζα. Τελικά η  έχει ακριβώς τρεις ρίζες.
έχει ακριβώς τρεις ρίζες.Έχουμε:
 συνεχής ως πράξεις συνεχών, συνεπώς διατηρεί πρόσημο στα διαφορετικά διαστήματα που χωρίζουν οι ρίζες της το
συνεχής ως πράξεις συνεχών, συνεπώς διατηρεί πρόσημο στα διαφορετικά διαστήματα που χωρίζουν οι ρίζες της το 
Η
 ικανοποιεί τις προυποθέσεις του Θ.Μ.Τ στα διαστήματα [1,ξ] και [ξ,2] συνεπώς υπάρχουν
ικανοποιεί τις προυποθέσεις του Θ.Μ.Τ στα διαστήματα [1,ξ] και [ξ,2] συνεπώς υπάρχουν  με
με 
τέτοια ώστε:
 και
και 
Συνεπώς για
 έχουμε
έχουμε  και για
και για  έχουμε
έχουμε  .
.Το πρόσημο της
 στα διαστήματα
στα διαστήματα  και
και  βρίσκεται εύκολα.
βρίσκεται εύκολα.Παρατήρηση: Παρόμοια άσκηση υπάρχει στο σχολικό βιβλίο σελ. 270 (άσκηση 6 Β΄Ομ) και τη θεωρώ μια από τις ωραιότερες της ενότητας.
Re: Μαθηματικά κατεύθυνσης 2014
Πολλά ερωτήματα του Γ και του Δ ήταν όρια με DLH. Το 2013 νομίζω δεν υπήρχε κανένα όριο.
Τα "καλά" θέματα εξαντλήθηκαν στην μονοτονία στις πράξεις και στα όρια.
Ας αφήσουμε τα συγχαρητήρια και ας απαιτήσουμε περισσότερη σοβαρότητα από εκείνους που βάζουν τα θέματα.
Τα "καλά" θέματα εξαντλήθηκαν στην μονοτονία στις πράξεις και στα όρια.
Ας αφήσουμε τα συγχαρητήρια και ας απαιτήσουμε περισσότερη σοβαρότητα από εκείνους που βάζουν τα θέματα.
ΠΑΥΛΟΣ
- S.E.Louridas
- Δημοσιεύσεις: 5963
- Εγγραφή: Σάβ Μαρ 21, 2009 10:53 am
- Τοποθεσία: Aegaleo.
- Επικοινωνία:
Re: Μαθηματικά κατεύθυνσης 2014
Μια και για το Δ2 είδαμε εκπληκτικές λύσεις εδώ στο mathematica ας δούμε και την εξής που κατά την άποψη μου θα μπορούσε να την επιχειρήσει ο Μαθητής καθότι είναι διδαγμένη μέθοδος παντού :
 οπότε αν η
οπότε αν η  είχε και άλλη ρίζα
είχε και άλλη ρίζα  θα υπήρχε
θα υπήρχε  ώστε
ώστε  που οδηγεί σε άτοπο διότι:
που οδηγεί σε άτοπο διότι: 
Όταν λοιπόν έχουμε
έχουμε  και
και 
καθότι και
και 

(*) Θα ήθελα να συστήσω στους Μαθητές που δίνουν τον δικό τους αγώνα να κλείσουν τα αυτιά τους σε πολλά απίθανα που ακούγονται, εδώ τα λένε και σε μας και επιμένουν... Άρα ξεχάστε αυτό το Μάθημα και πηγαίνετε μπροστά.
 οπότε αν η
οπότε αν η  είχε και άλλη ρίζα
είχε και άλλη ρίζα  θα υπήρχε
θα υπήρχε  ώστε
ώστε  που οδηγεί σε άτοπο διότι:
που οδηγεί σε άτοπο διότι: 
Όταν λοιπόν
 έχουμε
έχουμε  και
και 
καθότι
 και
και 

(*) Θα ήθελα να συστήσω στους Μαθητές που δίνουν τον δικό τους αγώνα να κλείσουν τα αυτιά τους σε πολλά απίθανα που ακούγονται, εδώ τα λένε και σε μας και επιμένουν... Άρα ξεχάστε αυτό το Μάθημα και πηγαίνετε μπροστά.
S.E.Louridas
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
Re: Μαθηματικά κατεύθυνσης 2014
Παρατηρήστε την εκφώνηση του θέματος Δ (το όριο που δίνει και το ερώτημα Δ2 των φετινών θεμάτων Προσομοίωσης 2014 (6-4-2014) της ΠΕΡΙΦΕΡΕΙΑΚΗΣ ΔΙΕΥΘΥΝΣΗΣ Β. ΑΙΓΑΙΟΥ Χ http://www.axortagos.gr/diagonisma-pros ... hinsi.html Ή ΚΑΙ ΕΔΩ http://issuu.com/6942663640/docs/______ ... __________και συγκρίνετε τα με την εκφώνηση του 4ου θέματος (τη συνάρτηση f) και το ερώτημα Δ2 ΤΩΝ ΣΗΜΕΡΙΝΩΝ ΘΕΜΑΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΤΕΥΘΥΝΣΗΣ (2-6-2014)....
Το σχόλιο μου: κοιτάτε κάτι συμπτώσεις που έχει η ζωή .....!!
Το σχόλιο μου: κοιτάτε κάτι συμπτώσεις που έχει η ζωή .....!!
- S.E.Louridas
- Δημοσιεύσεις: 5963
- Εγγραφή: Σάβ Μαρ 21, 2009 10:53 am
- Τοποθεσία: Aegaleo.
- Επικοινωνία:
Re: Μαθηματικά κατεύθυνσης 2014
Για το Δ3 θα μπορούσαμε να «διευκολύνουμε για λίγο τη ζωή μας» ως εξής:
 και να ασχοληθούμε με την
και να ασχοληθούμε με την  και
και  με ρίζες της τους αριθμούς
με ρίζες της τους αριθμούς  καθότι για την
καθότι για την  παίρνουμε
παίρνουμε 
 και μετά εύκολα πάμε στα
και μετά εύκολα πάμε στα  ...
...
 και να ασχοληθούμε με την
και να ασχοληθούμε με την  και
και  με ρίζες της τους αριθμούς
με ρίζες της τους αριθμούς  καθότι για την
καθότι για την  παίρνουμε
παίρνουμε 
 και μετά εύκολα πάμε στα
και μετά εύκολα πάμε στα  ...
...
τελευταία επεξεργασία από S.E.Louridas σε Τρί Ιουν 03, 2014 11:15 am, έχει επεξεργασθεί 1 φορά συνολικά.
S.E.Louridas
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
Re: Μαθηματικά κατεύθυνσης 2014
Απάντηση ενός μαθητή στο Δ3 :
Έχουμε![g'(x)=2(e^x - e)(x-2)[(x-1)e^x - e] g'(x)=2(e^x - e)(x-2)[(x-1)e^x - e]](/forum/ext/geomar/texintegr/latexrender/pictures/f9541d11f4b60d12e2d932b9271e9b2b.png) . Έστω η
. Έστω η  η οποία για
η οποία για  έχει σύνολο τιμών
έχει σύνολο τιμών  . Επίσης η
. Επίσης η  είναι αύξουσα στο
είναι αύξουσα στο  άρα υπάρχει μοναδικό
άρα υπάρχει μοναδικό  στο
στο  τέτοιο ώστε
τέτοιο ώστε  . Το
. Το  είναι διαφορετικό του
είναι διαφορετικό του  και του
και του  αφού
αφού  και
και  . Οπότε η
. Οπότε η 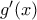 μηδενίζεται στα σημεία
μηδενίζεται στα σημεία  και
και  . Εξετάζουμε τις περιπτώσεις :
. Εξετάζουμε τις περιπτώσεις : Αν
Αν  η
η  θα έχει δύο τοπικά ελάχιστα και ένα τοπικό μέγιστο ,
θα έχει δύο τοπικά ελάχιστα και ένα τοπικό μέγιστο , Αν
Αν  όμοια θα έχει δύο τοπικά ελάχιστα και ένα τοπικό μέγιστο και
όμοια θα έχει δύο τοπικά ελάχιστα και ένα τοπικό μέγιστο και  Αν
Αν  επίσης θα έχει θα έχει δύο τοπικά ελάχιστα και ένα τοπικό μέγιστο.Σε κάθε περίπτωση έχουμε εξετάσει ότι το πρόσημο της
επίσης θα έχει θα έχει δύο τοπικά ελάχιστα και ένα τοπικό μέγιστο.Σε κάθε περίπτωση έχουμε εξετάσει ότι το πρόσημο της 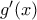 αλλάζει εκατέρωθεν τον ριζών της, οπότε η
αλλάζει εκατέρωθεν τον ριζών της, οπότε η  έχει δύο τοπικά ελάχιστα και ένα τοπικό μέγιστο.
έχει δύο τοπικά ελάχιστα και ένα τοπικό μέγιστο.
Έχουμε
![g'(x)=2(e^x - e)(x-2)[(x-1)e^x - e] g'(x)=2(e^x - e)(x-2)[(x-1)e^x - e]](/forum/ext/geomar/texintegr/latexrender/pictures/f9541d11f4b60d12e2d932b9271e9b2b.png) . Έστω η
. Έστω η  η οποία για
η οποία για  έχει σύνολο τιμών
έχει σύνολο τιμών  . Επίσης η
. Επίσης η  είναι αύξουσα στο
είναι αύξουσα στο  άρα υπάρχει μοναδικό
άρα υπάρχει μοναδικό  στο
στο  τέτοιο ώστε
τέτοιο ώστε  . Το
. Το  είναι διαφορετικό του
είναι διαφορετικό του  και του
και του  αφού
αφού  και
και  . Οπότε η
. Οπότε η 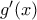 μηδενίζεται στα σημεία
μηδενίζεται στα σημεία  και
και  . Εξετάζουμε τις περιπτώσεις :
. Εξετάζουμε τις περιπτώσεις : Αν
Αν  η
η  θα έχει δύο τοπικά ελάχιστα και ένα τοπικό μέγιστο ,
θα έχει δύο τοπικά ελάχιστα και ένα τοπικό μέγιστο , Αν
Αν  όμοια θα έχει δύο τοπικά ελάχιστα και ένα τοπικό μέγιστο και
όμοια θα έχει δύο τοπικά ελάχιστα και ένα τοπικό μέγιστο και  Αν
Αν  επίσης θα έχει θα έχει δύο τοπικά ελάχιστα και ένα τοπικό μέγιστο.Σε κάθε περίπτωση έχουμε εξετάσει ότι το πρόσημο της
επίσης θα έχει θα έχει δύο τοπικά ελάχιστα και ένα τοπικό μέγιστο.Σε κάθε περίπτωση έχουμε εξετάσει ότι το πρόσημο της 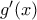 αλλάζει εκατέρωθεν τον ριζών της, οπότε η
αλλάζει εκατέρωθεν τον ριζών της, οπότε η  έχει δύο τοπικά ελάχιστα και ένα τοπικό μέγιστο.
έχει δύο τοπικά ελάχιστα και ένα τοπικό μέγιστο.Re: Μαθηματικά κατεύθυνσης 2014
ΔΕΚΤΟ σωστο. Αυτό όμως δειχνει απλοτητα; Μαλλον όχι. Ας σκεφτουμε το απλουστατο: Μονοτονια συν ριζα = προσημο. Μια απλη σκεψη δειχνει με απλο τροπο την εικονα. Εάν ο μαθητης ηταν δάσκαλος ποιος μαθητης του θα καταλαβαινε την σκεψη αυτή;Ανδρεας έγραψε:Απάντηση ενός μαθητή στο Δ3 :
Έχουμε. Έστω η
η οποία για
έχει σύνολο τιμών
. Επίσης η
είναι αύξουσα στο
άρα υπάρχει μοναδικό
στο
τέτοιο ώστε
. Το
είναι διαφορετικό του
και του
αφού
και
. Οπότε η
μηδενίζεται στα σημεία
και
. Εξετάζουμε τις περιπτώσεις :
Αν
η
θα έχει δύο τοπικά ελάχιστα και ένα τοπικό μέγιστο ,
Αν
όμοια θα έχει δύο τοπικά ελάχιστα και ένα τοπικό μέγιστο και
Αν
επίσης θα έχει θα έχει δύο τοπικά ελάχιστα και ένα τοπικό μέγιστο.Σε κάθε περίπτωση έχουμε εξετάσει ότι το πρόσημο της
αλλάζει εκατέρωθεν τον ριζών της, οπότε η
έχει δύο τοπικά ελάχιστα και ένα τοπικό μέγιστο.
Re: Μαθηματικά κατεύθυνσης 2014
Και γιατί να έχει 2 τοπικά ελάχιστα και 1 τοπικό μέγιστο και όχι το ανάποδο;
Στραγάλης Χρήστος
-
Επιτροπή Θεμάτων 14
- Δημοσιεύσεις: 6
- Εγγραφή: Τρί Μάιος 27, 2014 1:36 am
Re: Μαθηματικά κατεύθυνσης 2014
Αγαπητές/τοί φίλοι,
Παρακάτω βρίσκεται η 2η έκδοση των λύσεων των Θεμάτων στο μάθημα "Μαθηματικά Θετικής & Τεχνολογικής Κατεύθυνσης" του 2014 που επιμελήθηκε η Επιτροπή Θεμάτων 2014 του mathematica.gr.
EDIT: Προσθήκη της 2ης ανανεωμένης έκδοσης με σχόλια και επιπλέον λύσεις
Παρακάτω βρίσκεται η 2η έκδοση των λύσεων των Θεμάτων στο μάθημα "Μαθηματικά Θετικής & Τεχνολογικής Κατεύθυνσης" του 2014 που επιμελήθηκε η Επιτροπή Θεμάτων 2014 του mathematica.gr.
EDIT: Προσθήκη της 2ης ανανεωμένης έκδοσης με σχόλια και επιπλέον λύσεις
- Συνημμένα
-
- MATHEMATICA GR Μαθ Θετ Κατ Λύσεις Θεμάτων 2014 (2η έκδοση).pdf
- (883.4 KiB) Μεταφορτώθηκε 1761 φορές
Επιτροπή Θεμάτων 2014
Re: Μαθηματικά κατεύθυνσης 2014
Στο Δ3 έκανα το εξής. Είχα θέσει στο Δ1  , που χρειάζεται για την απόδειξη της μονοτονίας της
, που χρειάζεται για την απόδειξη της μονοτονίας της  . Μετά παρατήρησα πως είναι
. Μετά παρατήρησα πως είναι  . Έτσι, έχοντας δείξει από το Δ1 πως
. Έτσι, έχοντας δείξει από το Δ1 πως  , είπα πως αφού
, είπα πως αφού  γν. αύξουσα στο
γν. αύξουσα στο  και το όριό της στο
και το όριό της στο  είναι
είναι  , θα υπάρχει
, θα υπάρχει  , ώστε να ισχύει
, ώστε να ισχύει  , ενώ μετά έδειξα πως
, ενώ μετά έδειξα πως  , συνεχίζοντας με πίνακα προσήμων για να δείξω τη μονοτονία της
, συνεχίζοντας με πίνακα προσήμων για να δείξω τη μονοτονία της  και τα τοπικά ακρότατα που ζητούσε.
και τα τοπικά ακρότατα που ζητούσε.
 , που χρειάζεται για την απόδειξη της μονοτονίας της
, που χρειάζεται για την απόδειξη της μονοτονίας της  . Μετά παρατήρησα πως είναι
. Μετά παρατήρησα πως είναι  . Έτσι, έχοντας δείξει από το Δ1 πως
. Έτσι, έχοντας δείξει από το Δ1 πως  , είπα πως αφού
, είπα πως αφού  γν. αύξουσα στο
γν. αύξουσα στο  και το όριό της στο
και το όριό της στο  είναι
είναι  , θα υπάρχει
, θα υπάρχει  , ώστε να ισχύει
, ώστε να ισχύει  , ενώ μετά έδειξα πως
, ενώ μετά έδειξα πως  , συνεχίζοντας με πίνακα προσήμων για να δείξω τη μονοτονία της
, συνεχίζοντας με πίνακα προσήμων για να δείξω τη μονοτονία της  και τα τοπικά ακρότατα που ζητούσε.
και τα τοπικά ακρότατα που ζητούσε.Αν κάτι μπορεί να πάει στραβά, θα πάει!
Νόμος του Μέρφυ
Νόμος του Μέρφυ
-
Θεοδωρος Παγωνης
- Δημοσιεύσεις: 311
- Εγγραφή: Τετ Οκτ 26, 2011 2:10 pm
- Τοποθεσία: Αγρίνιο
Re: Μαθηματικά κατεύθυνσης 2014
Β1
Η λύση δεν είναι δική μου , είναι ενός μαθητή του φροντιστηρίου .
Είναι και
και  , άρα η εξίσωση
, άρα η εξίσωση  γράφεται :
γράφεται :

 , άρα οι μιγαδικοί
, άρα οι μιγαδικοί  είναι λύσεις της εξίσωσης
είναι λύσεις της εξίσωσης  , με
, με  και λύσεις
και λύσεις  .
.
Άρα , τελικά έχω :
Η λύση δεν είναι δική μου , είναι ενός μαθητή του φροντιστηρίου .
Είναι
 και
και  , άρα η εξίσωση
, άρα η εξίσωση  γράφεται :
γράφεται :
 , άρα οι μιγαδικοί
, άρα οι μιγαδικοί  είναι λύσεις της εξίσωσης
είναι λύσεις της εξίσωσης  , με
, με  και λύσεις
και λύσεις  .
.Άρα , τελικά έχω :

Re: Μαθηματικά κατεύθυνσης 2014
Το θέμα Γ1 έχει ξαναπέσει στα θέματα ομογενών του 2011 (θέμα Γ2). Έτυχε να έχω κάποιους μαθητές μετριότατους οπότε το είχαμε δει...
- Συνημμένα
-
- Panellinies-2011-omogeneis-mathkat_omo_11.pdf
- (150.17 KiB) Μεταφορτώθηκε 295 φορές
- S.E.Louridas
- Δημοσιεύσεις: 5963
- Εγγραφή: Σάβ Μαρ 21, 2009 10:53 am
- Τοποθεσία: Aegaleo.
- Επικοινωνία:
Re: Μαθηματικά κατεύθυνσης 2014
Επιτρέψτε μου να εκφράσω την μεγάλη μου χαρά που είμαι μέλος της οικογένειας mathematicα. Κατά την άποψη μου εκπληκτικές λύσεις με σαφή Μαθηματική και Διδακτική στόχευση και βέβαια με πλουραλισμό που δείχνει ότι τα Μαθηματικά τουλάχιστον δεν είναι "ταμπού", όπως εξάλλου και όλες οι παρεμβάσεις που πέρασαν από εδώ.Επιτροπή Θεμάτων 14 έγραψε:Αγαπητές/τοί φίλοι,
Παρακάτω βρίσκεται η 1η έκδοση των λύσεων των Θεμάτων στο μάθημα "Μαθηματικά Θετικής & Τεχνολογικής Κατεύθυνσης" του 2014 που επιμελήθηκε η Επιτροπή Θεμάτων 2014 του mathematica.gr.
τελευταία επεξεργασία από S.E.Louridas σε Τρί Ιουν 03, 2014 10:44 am, έχει επεξεργασθεί 1 φορά συνολικά.
S.E.Louridas
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
Re: Μαθηματικά κατεύθυνσης 2014
Από τα σχόλια της ΕΜΕ κρατάω δύο πράγματα:
1ο) Ότι είναι επιτέλους ένας σοβαρός σχολιασμός και όχι του τύπου" θέλω κάτι να πω, αλλά να μην το πω μήπως εκτεθώ",
2ο) Το σχόλιο με το οποίο κλίνει η ανακοίνωση:
Τέλος, τονίζουμε ότι πάγια θέση της Ελληνικής Μαθηματικής Εταιρείας είναι ότι η κλιμάκωση του βαθμού δυσκολίας των θεμάτων επιβάλλεται να είναι ίδια για όλα τα εξεταζόμενα μαθήματα.
Re: Μαθηματικά κατεύθυνσης 2014
Και εγώ ακριβώς το ίδιο αλλά αυτή η λύση με το θεώρημα μέγιστης ελάχιστης τιμής με άφησε άφωνο... πολύ έξυπνη!ArgirisM έγραψε:Στο Δ3 έκανα το εξής. Είχα θέσει στο Δ1, που χρειάζεται για την απόδειξη της μονοτονίας της
. Μετά παρατήρησα πως είναι
. Έτσι, έχοντας δείξει από το Δ1 πως
, είπα πως αφού
γν. αύξουσα στο
και το όριό της στο
είναι
, θα υπάρχει
, ώστε να ισχύει
, ενώ μετά έδειξα πως
, συνεχίζοντας με πίνακα προσήμων για να δείξω τη μονοτονία της
και τα τοπικά ακρότατα που ζητούσε.
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3347
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Μαθηματικά κατεύθυνσης 2014
Σωτήρη πολύ σωστά, και έχεις ταυτόχρονα αποδείξει και κάτι παραπάνω από την δοθείσα* κυρτότητα τηςS.E.Louridas έγραψε:Μια και για το Δ2 είδαμε εκπληκτικές λύσεις εδώ στο mathematica ας δούμε και την εξής που κατά την άποψη μου θα μπορούσε να την επιχειρήσει ο Μαθητής καθότι είναι διδαγμένη μέθοδος παντού :
οπότε αν η
είχε και άλλη ρίζα
θα υπήρχε
ώστε
που οδηγεί σε άτοπο διότι:

Όταν λοιπόνέχουμε
και

καθότικαι

 , την αυστηρή δηλαδή ανισότητα
, την αυστηρή δηλαδή ανισότητα  για
για  .
.*θα έπρεπε άραγε να είχε ζητηθεί από τους διαγωνιζόμενους να αποδείξουν την κυρτότητα της
 αντί να την υποθέσουν;
αντί να την υποθέσουν;Γιώργος Μπαλόγλου
Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
- S.E.Louridas
- Δημοσιεύσεις: 5963
- Εγγραφή: Σάβ Μαρ 21, 2009 10:53 am
- Τοποθεσία: Aegaleo.
- Επικοινωνία:
Re: Μαθηματικά κατεύθυνσης 2014
Γιώργο καλημέρα: ΝΑΙ συμφωνώ απόλυτα μαζί σου και τούτο και για την "τίμια" κατασκευαστική διαδικασία του θέματος.gbaloglou έγραψε: ...θα έπρεπε άραγε να είχε ζητηθεί από τους διαγωνιζόμενους να αποδείξουν την κυρτότητα τηςαντί να την υποθέσουν;
Γιώργος Μπαλόγλου
(*) Το "τίμια" προφανώς σε εισαγωγικά.
S.E.Louridas
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
Re: Μαθηματικά κατεύθυνσης 2014
Φοβερός αυτοσχεδιασμός δεδομένων των συνθηκών και έλλειψη μεθοδολογικής προσέγγισης...Θεοδωρος Παγωνης έγραψε:Β1
Η λύση δεν είναι δική μου , είναι ενός μαθητή του φροντιστηρίου .
Είναικαι
, άρα η εξίσωση
γράφεται :
, άρα οι μιγαδικοί
είναι λύσεις της εξίσωσης
, με
και λύσεις
.
Άρα , τελικά έχω :
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 17 επισκέπτες
