Θεωρούμε τρίγωνο
 με
με  .Έστω
.Έστω  σημεία των
σημεία των  τέτοια ώστε οι
τέτοια ώστε οι  να είναι διχοτόμοι των γωνιών
να είναι διχοτόμοι των γωνιών  αντίστοιχα.Έστω ότι ισχύει
αντίστοιχα.Έστω ότι ισχύει  .Έστω επίσης
.Έστω επίσης  .Αν οι περιγγεγραμμένοι κύκλοι των τριγώνων
.Αν οι περιγγεγραμμένοι κύκλοι των τριγώνων  και
και  τέμνονται στο
τέμνονται στο  να αποδειχθεί ότι τα σημεία
να αποδειχθεί ότι τα σημεία  είναι συνευθειακά.
είναι συνευθειακά.Πρόκειται για μια προσωπική σύνθεση κατά βάση.Την "ενίσχυσα" βασιζόμενος σε ένα πρόβλημα με το οποίο ασχολήθηκα πρόσφατα.Ελπίζω να μην υπάρχει ευκολότερη λύση από αυτή που έχω σκεφτεί.

 .
. τότε
τότε 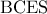 εγγράψιμο.
εγγράψιμο.

 που δίνει
που δίνει  εγγράψιμο.Έτσι
εγγράψιμο.Έτσι  που δίνει
που δίνει  εγγράψιμο και ολοκληρώνει την απόδειξη.
εγγράψιμο και ολοκληρώνει την απόδειξη.