Μία ακόμη αντιμετώπιση:
Αρχικά παρατηρούμε πως

(από το εγγεγραμμένο

). Άρα

.
Ισχύει

.
Όμως

και

αφού

. Άρα

(εφόσον

,

,

συνευθειακά).
Συνεπώς το τμήμα
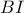
διχοτομεί την

. Θα δείξουμε ότι και το τμήμα

διχοτομεί την

Από το εγγεγραμμένο τετράπλευρο

λαμβάνουμε

,

,

και

.
Έτσι, από το τρίγωνο

έχουμε


. Το

είναι το έγκεντρο του
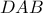
, άρα

. Από την

έχουμε


.
Στο σημείο αυτό θα προσπαθήσουμε να δείξουμε ότι τα τρίγωνα

και

είναι όμοια. Θεωρούμε το συμμετρικό του

ως προς το

. Το τετράπλευρο

είναι παραλληλόγραμμο, εφόσον οι διαγώνιοι διχοτομούνται.
Ισχύει

, άρα αρκεί να δείξουμε ότι τα σημεία

,

,

και

είναι ομοκυκλικά.
Εφαρμόζουμε σπειροειδή ομοιότητα με κέντρο

που στέλνει το

στο

. Ο μετασχηματισμός αυτός μας δίνει


Συνεπώς το τετράπλευρο

είναι εγγράψιμο. Ακόμη, η

συνδέει τα μέσα των

και

, άρα


. 'Ετσι:

. Εφόσον, λοιπόν,

και

θα είναι και


, δηλαδή το

είναι εγγράψιμο.
Άρα


. Συνεπώς το

είναι όμοιο με το

.Έστω

Από το τρίγωνο

έχουμε:

'Αρα


, δηλαδή η

διχοτομεί την

και το ζητούμενο έπεται.


- Egkentro.png (331.63 KiB) Προβλήθηκε 1077 φορές
 με
με  και έστω
και έστω  το μέσο της
το μέσο της  .
.  τέμνει τον κύκλο που διέρχεται από τα
τέμνει τον κύκλο που διέρχεται από τα  και
και  σε σημείο
σε σημείο  εσωτερικά του
εσωτερικά του  .
.  τέμνει τον κύκλο που διέρχεται από τα
τέμνει τον κύκλο που διέρχεται από τα  και
και  στα σημεία
στα σημεία  και
και  .
.  και
και  τέμνονται στο
τέμνονται στο  και οι ευθείες
και οι ευθείες  και
και  τέμνονται στο
τέμνονται στο  .
.  είναι το έγκεντρο του
είναι το έγκεντρο του  .
.
 προκύπτει ότι
προκύπτει ότι  διχοτόμος της
διχοτόμος της  του τριγώνου
του τριγώνου  .
. , όπως και
, όπως και 
 εγγράψιμο σε κύκλο διαμέτρου
εγγράψιμο σε κύκλο διαμέτρου  .
. στο σημείο
στο σημείο  προκύπτει ότι
προκύπτει ότι  είναι σημείο του ριζικού άξονα των δύο κύκλων (της κοινής τους χορδής) και με
είναι σημείο του ριζικού άξονα των δύο κύκλων (της κοινής τους χορδής) και με  ένα κοινό τους σημείο προκύπτει ότι
ένα κοινό τους σημείο προκύπτει ότι  είναι συνευθειακά, όπου
είναι συνευθειακά, όπου  .
. , (
, ( τα μέσα των
τα μέσα των  του τριγώνου
του τριγώνου  και με
και με  εγγράψιμο σε κύκλο άρα
εγγράψιμο σε κύκλο άρα  .
.
 του τριγώνου
του τριγώνου  θα είναι το έγκεντρό του και το ζητούμενο έχει αποδειχθεί.
θα είναι το έγκεντρό του και το ζητούμενο έχει αποδειχθεί. (από το εγγεγραμμένο
(από το εγγεγραμμένο  ). Άρα
). Άρα  .
. .
.  και
και  αφού
αφού  . Άρα
. Άρα (εφόσον
(εφόσον  ,
,  ,
, συνευθειακά).
συνευθειακά). 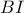 διχοτομεί την
διχοτομεί την  . Θα δείξουμε ότι και το τμήμα
. Θα δείξουμε ότι και το τμήμα  διχοτομεί την
διχοτομεί την 
 λαμβάνουμε
λαμβάνουμε  ,
,  ,
,  και
και  .
. έχουμε
έχουμε
 . Το
. Το  είναι το έγκεντρο του
είναι το έγκεντρο του 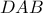 , άρα
, άρα . Από την
. Από την 
 .
. και
και  είναι όμοια. Θεωρούμε το συμμετρικό του
είναι όμοια. Θεωρούμε το συμμετρικό του  ως προς το
ως προς το  . Το τετράπλευρο
. Το τετράπλευρο  είναι παραλληλόγραμμο, εφόσον οι διαγώνιοι διχοτομούνται.
είναι παραλληλόγραμμο, εφόσον οι διαγώνιοι διχοτομούνται.  , άρα αρκεί να δείξουμε ότι τα σημεία
, άρα αρκεί να δείξουμε ότι τα σημεία  ,
,  ,
,  και
και  είναι ομοκυκλικά.
είναι ομοκυκλικά.  στο
στο  . Ο μετασχηματισμός αυτός μας δίνει
. Ο μετασχηματισμός αυτός μας δίνει 

 είναι εγγράψιμο. Ακόμη, η
είναι εγγράψιμο. Ακόμη, η  συνδέει τα μέσα των
συνδέει τα μέσα των  και
και  , άρα
, άρα 
 . 'Ετσι:
. 'Ετσι:  . Εφόσον, λοιπόν,
. Εφόσον, λοιπόν, και
και θα είναι και
θα είναι και 
 , δηλαδή το
, δηλαδή το  είναι εγγράψιμο.
είναι εγγράψιμο.
 . Συνεπώς το
. Συνεπώς το 
 έχουμε:
έχουμε: 

 , δηλαδή η
, δηλαδή η 