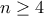 , να αποδειχθεί ότι μπορούμε να βρούμε στο επίπεδο
, να αποδειχθεί ότι μπορούμε να βρούμε στο επίπεδο 
σημεία
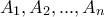 , τέτοια ώστε για το οποιοδήποτε σημείο
, τέτοια ώστε για το οποιοδήποτε σημείο  του επιπέδου, τουλάχιστον
του επιπέδου, τουλάχιστον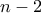 από τους
από τους αριθμούς
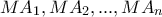 να είναι άρρητοι.
να είναι άρρητοι.Συντονιστές: cretanman, Demetres, polysot, socrates, silouan, rek2
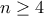 , να αποδειχθεί ότι μπορούμε να βρούμε στο επίπεδο
, να αποδειχθεί ότι μπορούμε να βρούμε στο επίπεδο 
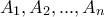 , τέτοια ώστε για το οποιοδήποτε σημείο
, τέτοια ώστε για το οποιοδήποτε σημείο  του επιπέδου, τουλάχιστον
του επιπέδου, τουλάχιστον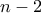 από τους
από τους 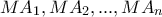 να είναι άρρητοι.
να είναι άρρητοι. με επαγωγή στο
με επαγωγή στο  .
. είναι άμεσο αφού δεν χρειάζεται να δείξουμε κάτι. Έστω λοιπόν ότι ισχύει για
είναι άμεσο αφού δεν χρειάζεται να δείξουμε κάτι. Έστω λοιπόν ότι ισχύει για  και έστω
και έστω  τα σημεία που επιλέξαμε.
τα σημεία που επιλέξαμε. το σύνολο όλων των σημείων του επιπέδου τα οποία έχουν ρητή απόστασή από ακριβώς δύο από τα
το σύνολο όλων των σημείων του επιπέδου τα οποία έχουν ρητή απόστασή από ακριβώς δύο από τα  .
.  είναι αριθμήσιμο. Πράγματι, αν ορίσουμε
είναι αριθμήσιμο. Πράγματι, αν ορίσουμε  τον κύκλο με κέντρο το
τον κύκλο με κέντρο το  και ακτίνα
και ακτίνα 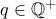 , τότε το
, τότε το  είναι το σύνολο όλων των σημείων που ανήκουν σε τουλάχιστον δύο από τους
είναι το σύνολο όλων των σημείων που ανήκουν σε τουλάχιστον δύο από τους  . Μόνο που το πλήθος των
. Μόνο που το πλήθος των  είναι αριθμήσιμο, και κάθε δύο τέτοιοι κύκλοι έχουν το πολύ δύο σημεία τομής. Άρα όντως το
είναι αριθμήσιμο, και κάθε δύο τέτοιοι κύκλοι έχουν το πολύ δύο σημεία τομής. Άρα όντως το  είναι αριθμήσιμο.
είναι αριθμήσιμο. αρκεί να επιλέξουμε ως
αρκεί να επιλέξουμε ως  ένα σημείο του επιπέδου το οποίο δεν έχει επιλεχθεί και το οποίο δεν έχει ρητή απόσταση από κανένα σημείο του
ένα σημείο του επιπέδου το οποίο δεν έχει επιλεχθεί και το οποίο δεν έχει ρητή απόσταση από κανένα σημείο του  .
.  αριθμήσιμο υποσύνολο του επιπέδου, τότε υπάρχει σημείο
αριθμήσιμο υποσύνολο του επιπέδου, τότε υπάρχει σημείο  του επιπέδου το οποίο έχει άρρητη απόσταση από όλα τα σημεία του
του επιπέδου το οποίο έχει άρρητη απόσταση από όλα τα σημεία του  . [Μετά παίρνουμε
. [Μετά παίρνουμε 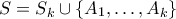 για να αποφύγουμε την επιλογή των
για να αποφύγουμε την επιλογή των  και τελειώσαμε.]
και τελειώσαμε.] μπορούμε να βρούμε σε οποιαδήποτε ευθεία
μπορούμε να βρούμε σε οποιαδήποτε ευθεία 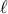 του επιπέδου. Πράγματι για κάθε σημείο
του επιπέδου. Πράγματι για κάθε σημείο  του
του  , και κάθε ρητή απόσταση
, και κάθε ρητή απόσταση  υπάρχουν το πολύ δύο σημεία της
υπάρχουν το πολύ δύο σημεία της 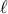 με απόσταση ίση με
με απόσταση ίση με  από το
από το  . Άρα μόνο πεπερασμένα σημεία της
. Άρα μόνο πεπερασμένα σημεία της 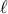 έχουν ρητή απόσταση από κάποιο σημείο της
έχουν ρητή απόσταση από κάποιο σημείο της  .
.Πολλή κομψή η κατασκευή του Δημήτρη.s.kap έγραψε:Δοθέντος ενός φυσικού αριθμού, να αποδειχθεί ότι μπορούμε να βρούμε στο επίπεδο

σημεία, τέτοια ώστε για το οποιοδήποτε σημείο
του επιπέδου, τουλάχιστον
από τους
αριθμούςνα είναι άρρητοι.
 τα σημεία
τα σημεία ![\displaystyle{A_1= \sqrt [3] 2 , \, A_2= 2\sqrt [3] 2 , \, A_3=3\sqrt [3] 2 , \, ... } \displaystyle{A_1= \sqrt [3] 2 , \, A_2= 2\sqrt [3] 2 , \, A_3=3\sqrt [3] 2 , \, ... }](/forum/ext/geomar/texintegr/latexrender/pictures/6f0674da741e70c9c0e81316fe46ea59.png) . Ισχυρίζομαι ότι κάνουν την δουλειά.
. Ισχυρίζομαι ότι κάνουν την δουλειά. 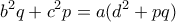 (βλέπε σχήμα).
(βλέπε σχήμα).  οι
οι 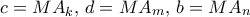 με
με 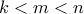 ήσαν (και οι τρεις) ρητοί. Τότε από Stewart
ήσαν (και οι τρεις) ρητοί. Τότε από Stewart![\displaystyle{b^2(n-m)\sqrt [3] 2+ c^2(m-k)\sqrt [3] 2=(n-k)\sqrt [3] 2\left (d^2+(n-m)\sqrt [3] 2\cdot (m-k)\sqrt [3] 2\right )} \displaystyle{b^2(n-m)\sqrt [3] 2+ c^2(m-k)\sqrt [3] 2=(n-k)\sqrt [3] 2\left (d^2+(n-m)\sqrt [3] 2\cdot (m-k)\sqrt [3] 2\right )}](/forum/ext/geomar/texintegr/latexrender/pictures/e5f3f97549d2909de62627db983d7310.png)
![\displaystyle{\sqrt [3] 2} \displaystyle{\sqrt [3] 2}](/forum/ext/geomar/texintegr/latexrender/pictures/02e13013edcbb65dfbc1a059bf8e2270.png) γράφεται
γράφεται ![\displaystyle{b^2(n-m)+ c^2(m-k)=(n-k)\left (d^2+(n-m)(m-k)\sqrt [3] 4\right )} \displaystyle{b^2(n-m)+ c^2(m-k)=(n-k)\left (d^2+(n-m)(m-k)\sqrt [3] 4\right )}](/forum/ext/geomar/texintegr/latexrender/pictures/9a63484b4ee3c5793dd6fd81f41ddb1b.png) .
. 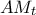 που είναι ρητοί, όπως θέλαμε.
που είναι ρητοί, όπως θέλαμε. όχι μόνο το πολύ δύο από τους
όχι μόνο το πολύ δύο από τους 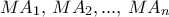 είναι ρητοί αλλά το πολύ δύο από τους
είναι ρητοί αλλά το πολύ δύο από τους 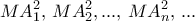 είναι ρητοί.
είναι ρητοί. όπου
όπου 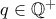 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες