Απίστευτο μέσο

[KARKAR]

Τρίγωνο είναι εγγεγραμμένο σε κύκλο . Η εφαπτομένη στο αντιδιαμετρικό

σημείο της κορυφής , τέμνει την προέκταση της στο σημείο .

Αν η τέμνει τις πλευρές στα αντίστοιχα , δείξτε ότι : .

[silouan]

Εδώ το είχα χρησιμοποιήσει σαν λήμμα με απόδειξη μέσω του θεωρήματος Pascal.
http://mathematica.gr/forum/viewtopic.p ... cal#p72300

Εδώ υπάρχει και συνθετική λύση
viewtopic.php?f=22&t=12476&p=72016#p72016

[KARKAR]

Μία διαφορετική και εξαιρετική λύση ( όχι δική μου ) ...

Αν το μέσο της επειδή , , τα είναι ομοκυκλικά .

Από το εγγράψιμο λοιπόν , παίρνω την ισότητα των μωβ γωνιών . Ίσες είναι προφανώς

επίσης , οι πράσινες και οι μπλε γωνίες , συνεπώς και .

Έτσι : και . Αλλά τα δεύτερα μέλη είναι ίσα ,

οπότε : , δηλαδή ,

[AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ]

Πρόκειται για πρόταση από το έργο του Πάππου "Συναγωγή" και μεταξύ άλλων, συμπεριλήφθηκε σε ανακοίνωση του κυρίου Βασιλη Καρασμάνη στο "Α' Πανελλήνιο Συνέδριο Ιστορίας και Φιλοσοφίας των Μαθηματικών", το 1989 στην Αθήνα (Εθνικό Ίδρυμα Ερευνών). Σίγουρα ο Μιχάλης ο Λάμπρου μπορεί να μας διαφωτίσει περισσότερο.
Καταθέτω και τη δική μου απόδειξη:
Αρκεί να αποδείξουμε ότι οι και η παράλληλη από το προς την , αποτελούν αρμονική δέσμη.
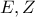Έστω οι παράλληλες προβολές προς τις αντίστοιχα, του πάνω στην .
Από την ισότητα των μπλέ και κόκκινων γωνιών (λόγω συμμετριών ως προς τις μεσοκάθετες των αντίστοιχα), οι ευθείες αποτελούν επίσης αρμονική δέσμη, αφού η διχοτομεί τη γωνία των και είναι κάθετη στην . Οπότε και οι αποτελούν αρμονική δέσμη, άρα το ίδιο ισχύει και για τις παράλληλές τους από το .

[vittasko]

Στο σχήμα του Θανάση ( KARKAR ) πιο πάνω, ο κύκλος έστω με διάμετρο το περνάει από το και επανατέμνει τον κύκλο στο σημείο έστω

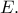
Η ευθεία είναι η πολική του σημείου ως προς τον κύκλο και θεωρούμε την ευθεία ως τυχούσα τέμνουσα τον ίδιο κύκλο.

Άρα, το τετράπλευρο είναι αρμονικό και επομένως, η δέσμη είναι αρμονική.

Επειδή τώρα, ισχύει , λόγω της διαμέτρου στον κύκλο , και , λόγω της πολικότητας του ως προς τον προκύπτει ότι

Από , λόγω της αρμονικής δέσμης , συμπεραίνεται ότι και το ζητούμενο έχει αποδειχθεί.

Κώστας Βήττας.

[MAnTH05]

Μερικές ιδέες για εναλλακτική απόδειξη

Αν ορίσουμε το ως την τομή της εκ του παράλληλη στην με την και αντίστοιχα το
και έστω η τομή της με την
το ζητούμενο είναι ισοδύναμο με το να αποδείξουμε ότι η εφάπτεται του
Έστω ότι οι ευθείες και τέμνουν την στα και αντίστοιχα.
Είναι
Άρα
Όμως
Άρα θέλουμε ν.δ.ο
Ισχυριζόμαστε ότι το τετράπλευρο είναι εγγράψιμο.
Αυτό ισχύει αν και μόνο αν το σημείο Miquel του ανήκει στη διαγώνιο .
Οπότε παίρνουμε την τομή του με την έστω και δείχνουμε ότι τα σημεία , , , είναι ομοκυκλικά.
Είναι
Έτσι μπορούμε να ολοκληρώσουμε την απόδειξη δείχνοντας ότι τα τρίγωνα και είναι όμοια π.χ. με σύνθεση στροφής και ομοιοθεσίας με κέντρο το , γωνία και λόγο
Επομένως όπως θέλαμε.

πρόταση Πάππου.png (383.65 KiB) Προβλήθηκε 937 φορές