Πανέμορφη Γεωμετρική συμμετρία
Συντονιστές: cretanman, Demetres, polysot, socrates, silouan, rek2
- Σεραφείμ
- Επιμελητής
- Δημοσιεύσεις: 1872
- Εγγραφή: Τετ Μάιος 20, 2009 9:14 am
- Τοποθεσία: Θεσσαλονίκη - Γιάννενα
Πανέμορφη Γεωμετρική συμμετρία
Οι τριχοτόμοι τυχαίου τριγώνου, τεμνόμενες ανα δύο, σχηματίζουν πάντα ισόπλευρο τρίγωνο.
- Συνημμένα
-
- Trixotomoi.jpg (18.88 KiB) Προβλήθηκε 3379 φορές
Σεραφείμ Τσιπέλης
Re: Πανέμορφη Γεωμετρική συμμετρία
Δεν την απεφυγα τελικα την τριγωνομετρια...
Εστω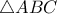 το αρχικο τριγωνο και
το αρχικο τριγωνο και 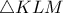 το εσωτερικο (οι
το εσωτερικο (οι 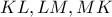 αντιστοιχουν στις
αντιστοιχουν στις  αντιστοιχα). Επισης, για τις γωνιες, θετουμε
αντιστοιχα). Επισης, για τις γωνιες, θετουμε 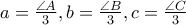 .
.
Αν ειναι η ακτινα του περιγεγραμμενου κυκλου του
ειναι η ακτινα του περιγεγραμμενου κυκλου του 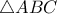 , εχουμε (απο νομο ημιτονων στο
, εχουμε (απο νομο ημιτονων στο  )
) 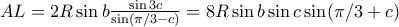 (μετα απο χρηση τριγωνομετριας στο κλασμα). Ομοιως
(μετα απο χρηση τριγωνομετριας στο κλασμα). Ομοιως 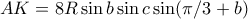 . Ετσι,
. Ετσι, 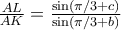 .
.
Βλεπουμε λοιπον οτι, στο τριγωνο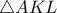 ισχυει
ισχυει 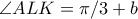 και
και 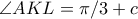 (αφου
(αφου 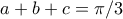 ). Παιρνοντας τις αντιστοιχες γωνιες για τα αλλα τριγωνα (
). Παιρνοντας τις αντιστοιχες γωνιες για τα αλλα τριγωνα (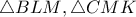 ) καταληγουμε στο συμπερασμα οτι καθε γωνια του
) καταληγουμε στο συμπερασμα οτι καθε γωνια του 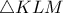 ισουται με
ισουται με 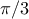 .
.
Δημητρης Σκουτερης
Εστω
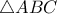 το αρχικο τριγωνο και
το αρχικο τριγωνο και 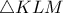 το εσωτερικο (οι
το εσωτερικο (οι 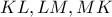 αντιστοιχουν στις
αντιστοιχουν στις  αντιστοιχα). Επισης, για τις γωνιες, θετουμε
αντιστοιχα). Επισης, για τις γωνιες, θετουμε 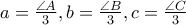 .
.Αν
 ειναι η ακτινα του περιγεγραμμενου κυκλου του
ειναι η ακτινα του περιγεγραμμενου κυκλου του 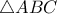 , εχουμε (απο νομο ημιτονων στο
, εχουμε (απο νομο ημιτονων στο  )
) 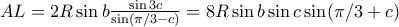 (μετα απο χρηση τριγωνομετριας στο κλασμα). Ομοιως
(μετα απο χρηση τριγωνομετριας στο κλασμα). Ομοιως 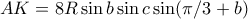 . Ετσι,
. Ετσι, 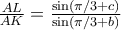 .
.Βλεπουμε λοιπον οτι, στο τριγωνο
 ισχυει
ισχυει 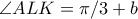 και
και 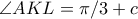 (αφου
(αφου 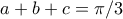 ). Παιρνοντας τις αντιστοιχες γωνιες για τα αλλα τριγωνα (
). Παιρνοντας τις αντιστοιχες γωνιες για τα αλλα τριγωνα (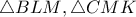 ) καταληγουμε στο συμπερασμα οτι καθε γωνια του
) καταληγουμε στο συμπερασμα οτι καθε γωνια του 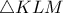 ισουται με
ισουται με 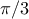 .
.Δημητρης Σκουτερης
Δημήτρης Σκουτέρης
Τα μαθηματικά είναι η μοναδική επιστήμη που θα μπορούσε κανείς να εξακολουθήσει να ασκεί αν κάποτε ξυπνούσε και το σύμπαν δεν υπήρχε πλέον.
Τα μαθηματικά είναι η μοναδική επιστήμη που θα μπορούσε κανείς να εξακολουθήσει να ασκεί αν κάποτε ξυπνούσε και το σύμπαν δεν υπήρχε πλέον.
-
Μπάμπης Στεργίου
- Επιμελητής
- Δημοσιεύσεις: 5561
- Εγγραφή: Δευ Δεκ 22, 2008 2:16 pm
- Τοποθεσία: Χαλκίδα - Καρδίτσα
Re: Πανέμορφη Γεωμετρική συμμετρία
Δημήτρη , ποτέ δεν αξιώθηκα να συγκεντρώσω όλες τις αποδείξεις που είναι γνωστές στο περίφημο αυτό θεώρημα του Morley ! Αν βρεις το χρόνο να ξεκινήσεις κάτι τέτοιο, να σου στείλω και τις πηγές ! Θα αξίζει τον κόπο !dement έγραψε:Δεν την απεφυγα τελικα την τριγωνομετρια...
Εστωτο αρχικο τριγωνο και
το εσωτερικο (οι
αντιστοιχουν στις
αντιστοιχα). Επισης, για τις γωνιες, θετουμε
.
Ανειναι η ακτινα του περιγεγραμμενου κυκλου του
, εχουμε (απο νομο ημιτονων στο
)
(μετα απο χρηση τριγωνομετριας στο κλασμα). Ομοιως
. Ετσι,
.
Βλεπουμε λοιπον οτι, στο τριγωνοισχυει
και
(αφου
). Παιρνοντας τις αντιστοιχες γωνιες για τα αλλα τριγωνα (
) καταληγουμε στο συμπερασμα οτι καθε γωνια του
ισουται με
.
Δημητρης Σκουτερης
Μπάμπης
- Σεραφείμ
- Επιμελητής
- Δημοσιεύσεις: 1872
- Εγγραφή: Τετ Μάιος 20, 2009 9:14 am
- Τοποθεσία: Θεσσαλονίκη - Γιάννενα
Re: Πανέμορφη Γεωμετρική συμμετρία
Γεωμετρική
- Συνημμένα
-
- Solution2.jpg (123.58 KiB) Προβλήθηκε 3045 φορές
Σεραφείμ Τσιπέλης
-
Μπάμπης Στεργίου
- Επιμελητής
- Δημοσιεύσεις: 5561
- Εγγραφή: Δευ Δεκ 22, 2008 2:16 pm
- Τοποθεσία: Χαλκίδα - Καρδίτσα
Re: Πανέμορφη Γεωμετρική συμμετρία
Αυτή είναι μια πολύ ωραία λύση !
Είχα τη λύση στα βιβλία α) Johnson : Advanced Euclidean Geometry(Dover), β) Τσιντσιφας : Γεωμετρία γ) Μαραγκάκης :Γεωμετρικά θέματα ,δ) Coxeter : Geometry revisited , αλλά αυτή δεν τη θυμόμουνα .
Είχα μελετήσει παλαιότερα και τις λύσεις στο Cut the Knot, αλλά δεν τις έχω κρατήσει στο αρχείο μου . Αν κάποιος βρει συντομότερη λύση, ας μας τη στείλλει.
Είχα τη λύση στα βιβλία α) Johnson : Advanced Euclidean Geometry(Dover), β) Τσιντσιφας : Γεωμετρία γ) Μαραγκάκης :Γεωμετρικά θέματα ,δ) Coxeter : Geometry revisited , αλλά αυτή δεν τη θυμόμουνα .
Είχα μελετήσει παλαιότερα και τις λύσεις στο Cut the Knot, αλλά δεν τις έχω κρατήσει στο αρχείο μου . Αν κάποιος βρει συντομότερη λύση, ας μας τη στείλλει.
-
zorba_the_freak
- Δημοσιεύσεις: 117
- Εγγραφή: Κυρ Μάιος 31, 2009 7:13 pm
- Τοποθεσία: στην οθόνη σου
Re: Πανέμορφη Γεωμετρική συμμετρία
Δες και εδώ:
1) http://mathworld.wolfram.com/MorleysTheorem.html
2) http://en.wikipedia.org/wiki/Morley%27s ... or_theorem
3) http://www.cut-the-knot.org/triangle/Morley/
4) http://agutie.homestead.com/FiLEs/morley.html
5) http://www.geocities.com/SoHo/Exhibit/8 ... orley.html
1) http://mathworld.wolfram.com/MorleysTheorem.html
2) http://en.wikipedia.org/wiki/Morley%27s ... or_theorem
3) http://www.cut-the-knot.org/triangle/Morley/
4) http://agutie.homestead.com/FiLEs/morley.html
5) http://www.geocities.com/SoHo/Exhibit/8 ... orley.html
- Σεραφείμ
- Επιμελητής
- Δημοσιεύσεις: 1872
- Εγγραφή: Τετ Μάιος 20, 2009 9:14 am
- Τοποθεσία: Θεσσαλονίκη - Γιάννενα
Re: Πανέμορφη Γεωμετρική συμμετρία
Μία ακόμα λύση ...
- Συνημμένα
-
- Tri-Solution.jpg (197.24 KiB) Προβλήθηκε 2824 φορές
Σεραφείμ Τσιπέλης
Re: Πανέμορφη Γεωμετρική συμμετρία
Νομίζω ότι η σωστή διατύπωση του θεωρήματος της ανάρτησης (που αναφέρεται στο θεώρημα Morley) πρέπει να είναι:Οι τριχοτόμοι τυχαίου τριγώνου, τεμνόμενες ανα δύο, σχηματίζουν πάντα ισόπλευρο τρίγωνο.
Οι τριχοτόμοι τυχαίου τριγώνου, πλησιέστερες στις πλευρές, τέμνονται στις κορυφές ισοπλεύρου τριγώνου.
Η κάθε γωνία ενός τριγώνου έχει δυο τριχοτόμους. Έτσι οι τριχοτόμοι δύο γωνιών τέμνονται σε 4 σημεία. Άρα οι τριχοτόμοι των τριών γωνιών τέμνονται σε 3x4 = 12 σημεία. Επομένως οι τριχοτόμοι των τριών γωνιών τέμνονται σε 12 σημεία. Συνεπώς υπάρχουν C(12,3) = 220 τρίγωνα με κορυφές σημεία τομής τριχοτόμων. Εξ αυτών μόνο το τρίγωνο με κορυφές τις τομές των τριχοτόμων, πλησιέστερων στις πλευρές, είναι ισόπλευρο.
Σπύρος Κουρούκλης
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες
